【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
1.慣性力
ここまで特殊相対性理論について話をしてきたのだが、特殊相対性理論の「特殊」とは何なのかを振り返っておこう。
特殊相対論に登場した原理の一つに、「特殊相対性原理」というものがあった。これは、いかなる慣性系にいる物体にとっても、物理法則は同じである、という原理である。このことを認めれば、どんな慣性系にいるものにとっても、自らの絶対速度はわからない、ということが言えて、従って絶対静止している慣性系は存在しないことが導かれたのである。
このことから、($E=m_0c^2$)という、「質量」と「エネルギー」の等価性も結論づけられたのが、前章の結論の一つであった。
物理学とは信ずるものではない。もし、物理学者が信ずるものがあるとすれば、それは「この宇宙には、物理法則が存在し、時間、空間を越えて通用する」という仮定である。
そうであるならば、相対性理論が適用できるのは慣性系だけである、という条件は、物理学者にとって非常に不満である。「いかなる運動をしている物体にとっても、物理法則は同じである」という原理を採用したいのである。
この原理を「一般相対性原理」と呼ぶ。
慣性系にいない物体が、慣性系にいる物体と決定的に異なる点を確認しておこう。非慣性系では、物体は外部から力を受けて、その速度を変化させることがそれである。
あなたは、今、電車の中に立っている、そう考えてもらいたい。
もし電車が走っていなければ、電車とあなたは慣性系にいる。だから、手から離れたボールは、自分の真下に落下し、また自分の手元に戻ってくる。これは、電車が時速$80km$で等速直線運動していても同じである。やはりあなたと電車は慣性系にいるのであり、手から離れたボールは、自分の真下に落下し、また自分の手元に戻ってくる。(だからこそ、電車の外の景色を見なければ、あなた自身は、電車が時速何$km$で走っているのかを知る手段がないのである。)
しかし、電車が加速していたら、そうは行かない。あなたの手を離れたボールは、電車に対して相対加速度を持つので、電車の床へ直線的に落下しない。電車の進行方向と逆へ引っ張られているように動く。外部からの力で加速しているのは電車であるのに、まるで力を受けているのがボールであるかのように、ボールは動くのである。
ちょっと注意していただきたい。このように、慣性系と加速系では、物理現象が異なる。つまり、加速系では、そこにある物体に力が働いて、物体が加速しているように観測されるということである。
力を受けていないのに、力を受けているかのように動くのは、ボールだけではない。実は、電車の中に立っているあなた自身も事情は同じなのである。電車が動き出すとき(停車するとき)、電車は加速(減速)する。このとき、あなたが、体を後ろへ(前へ)引っ張られるのは、あなたが経験したことのはずだ。
この事柄に対し、私たちが選ぶべき決断は二つである。
(1)加速系と慣性系は物理法則が違っているのだ、と諦める当たり前なのであるが、物理学者は、(2)を選択する。
(2)それでも、物理法則は同じであると言い得る道を模索する
力が働いていないのに、物体が加速するのが物理法則に反するのであれば、力が働いて加速していると考えればよい。この発想を「慣性力」と呼ぶ。
つまり、相対加速という考えを捨て、実際に慣性力という名の力が働いて物体がその速度を変えているのだとすれば、物理法則はこれまで通りなのである。
一言いいたい!

【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
2.慣性力と重力
次のようなケースを考えてほしい。(図15-1参照)
宇宙空間にロケットが止まっている。当然無重力である。ロケットの中には束縛されていないボールが一個ある。図では、ゴム紐で束縛しているように見えるが、単にボールの動きを見やすくするために、書いてあるに過ぎないと考えてもらいたい。
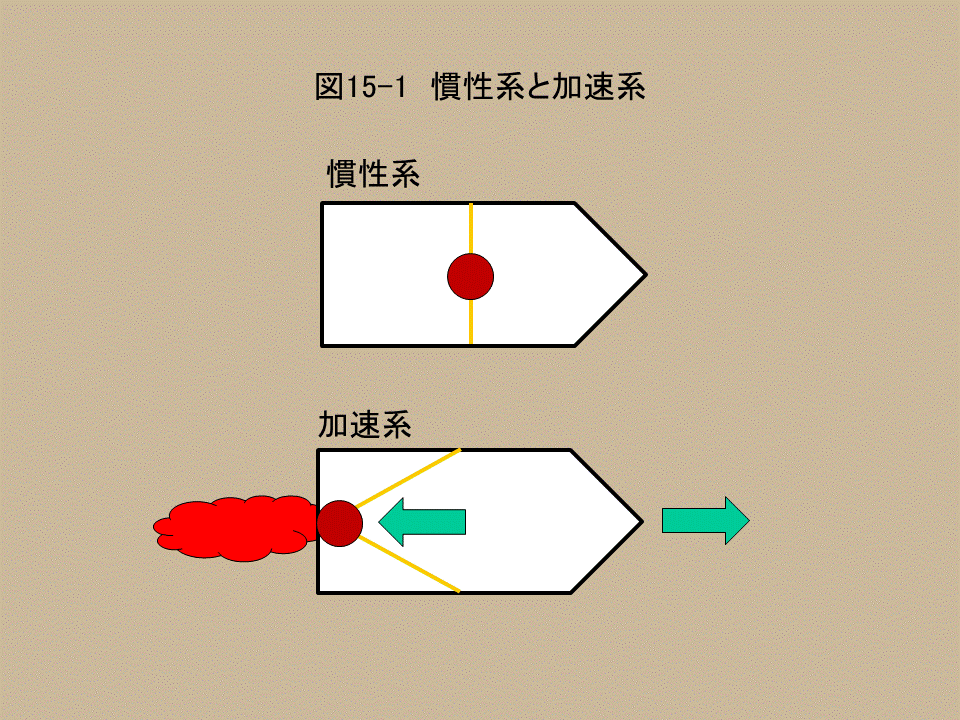
慣性系においては、ボールはロケット内に浮いており、何も力は働かず、ロケットに対して動くこともない。(上図:慣性系)
ここで、ロケットが燃料を噴射して、加速を開始する。そうすると、ロケット内のボールには、ロケットの進行方向とは逆向きに慣性力が加わり加速するので、ボールは動き出し、ロケットの向かって左面に押しつけられる結果となる。わかりますね。(下図:加速系)
しかし、ロケットが動き出す前に、ロケットの外から見ていた人にとっては、この現象は次のように見えるはずだ。
加速しているのはロケットである。ロケットは燃料を噴射することで、反作用で力を受け、その速度を変えているのだ。しかしながら、ロケット側に立って見れば、力を受けているのは、ボールの方である。
ロケット内のボールに力は働かず、慣性系にあるので、その場にとどまろうとする。このため動いたロケットから見て、ロケットの左面に押しつけられる。
つまり、加速するロケット内のボールに加わる力は、見る者の立場によって、現れたり消えたりするおかしな力なのである。
話を変えて、全く異なる状況を考える。(図15-2参照)
地球があって、その地表に静止して立っているロケットを考える。ロケットは地表に静止しており、その中にあるボールにも重力が働くので、下方への力でボールは床に押しつけられる。(右図:重力系)
対して、地球上空から自由落下しているロケット内では、ロケットもボールも一緒に落ちているので、両者に力は感じられない。(左図:慣性系)
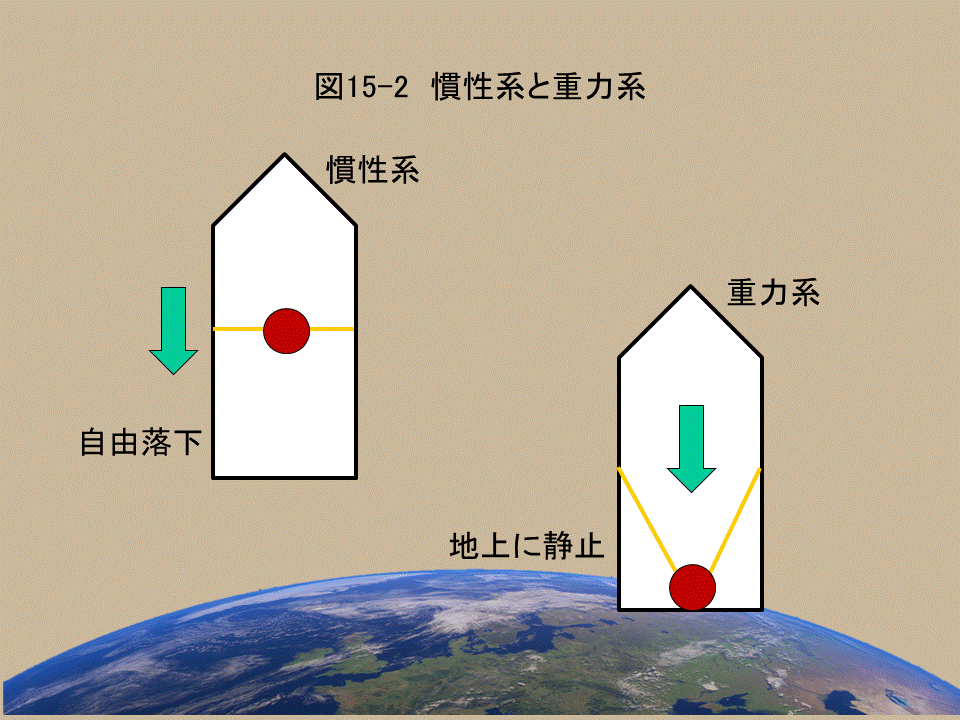
普段、私たちは、自由落下を加速系と考えることに慣れている。だって、ロケットもボールも地球に引かれて落下という加速度運動をしていると見るのだから。
そして、地表に静止している状態を慣性系と見る。なぜなら、力が働かず、ロケットもボールも地表に静止しているのだから。
この場合も、重力は、地上にいる者と自由落下しているものにとって、現れたり消えたりする見かけの力であることに注意して貰いたい。
ここで、指摘する。
ロケットとロケット内にいるボールにとって、図15-2は、図15-1を反時計回りに90度回転させただけである。という事実だ。
読者のみなさん、正念場である。大変な発想の転換が必要だ。
アインシュタインは、ロケット(及びロケットと共に加速する者)にとって、図15-1と図15-2の状態は区別できない、と考えた。いわゆる、思考実験によって、そのように結論したのだ。
この結論に従えば、宇宙空間を加速するロケットと、地球表面に静止するロケットとは、どちらの状態にいるのか区別できない、ということになる。つまり、もし物体が、慣性力または重力を受ける空間では、それが慣性力なのか重力なのか区別不可能ということだ。
同様に、宇宙空間で加速していないロケットと、地表へ向かって自由落下しているロケットは、同じ慣性系として区別できないことにもなる。
この結論を前提として取り入れ、アインシュタインは、一般相対性理論を構築することになる。
加速系と、重力系を区別できないことを、等価原理と呼ぶ。
そして、物理学者が目指した、「いかなる運動をしている物体にとっても、物理法則は同一である」という仮定を、一般相対性原理と呼んだ。
「いかなる運動をしている物体にとっても、物理法則は同一である」ことが、なぜ一般相対性原理なのか、と疑問を持った人がいるはずである。説明しておこう。
ある系(閉じた部屋)にいる者にとって、全く力を感じない系を、慣性系とよび、何らかの力を感じる場合、その系は、加速しているか、重力の働く場所にいるかどちらかである。ということである。
力とは、以下の式で示される。 \begin{eqnarray} F=ma \end{eqnarray} ($F$)は力、($m$)は質量、($a$)は加速度である。
上式は、力($F$)は、質量($m$)の物体に、加速度($a$)の速度変化を与える、と読むことができる。
もし、加速度がゼロだったら、力もゼロとなり、これは慣性系に他ならない。だから、慣性系というのは加速度がゼロという加速系の特別なケースと考えていい。
従って、一般相対論が指す一般相対性原理の物理法則とは、その系にいる物体が力を受けるとき、その系は加速系ないしは重力系にいる、ということである。
ここで、加速系ないしは重力系と繰り返すのは、非常に面倒であり、またこの二つは区別できないのだから、これを同じに記述する数学があれば、あえて二つをわけて考える必要はないことになる。
アインシュタインはこの数学を探し求め、たどり着いたのが、リーマン幾何学である。
特殊相対論が前提としたのは、平らな4次元時空間であり、これを記述したのは、ユークリッド幾何学という。(何のことはない、私たちが小学校から習っている幾何学である。)
「ユークリッド幾何学」は、五つの公理・公準から構築される数学で、公理の第1番目は、「同じものと等しいものは互いに等しい」である。「なんぼなんでもそのくらいわかるわい!」と言うなかれ。「リーマン幾何学」とは「曲がった時空間」を考えるので、我々があたりまえと思っていることさえ通用しない世界なのである。
一言いいたい!

【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
3.一般相対論の結論
「リーマン幾何学」を理解するには、テンソル解析という微分幾何学を理解する必要があるのだが、私はそんなことをここで説明する気はないし、あってもできない。
リーマンとは人名(19世紀なかばの人)であるが、彼が作ったリーマン幾何学は、彼の生前にはほとんど評価されることはなかった。理由は、リーマン幾何学が理論的に間違っていたからではない。真面目に研究しても、何の役にも立たなかったからだ。
アインシュタインが一般相対論を記述するのに最も適した数学として、これを発掘したのである。
さわりだけ、ちょっと書くと、「三角形の内角の和は二直角である」というのは典型的なユークリッド幾何学であり、「三角形の内角の和は必ずしも二直角ではない」というのがリーマン幾何学である。そんなバカな、と思う人は、地球上で、赤道の一部を底辺とし、北極を頂点とする三角形を考えてください。底辺が作る二つの角だけで二直角になり、頂角は、0〜360度の間で任意だ。
何を言っている、地球の表面は平面じゃないからそうなるのであって、平面なら二直角になるに決まっている、と反論する人がいるかもしれない。
勘違いをしてはいけない。平面しか扱わない幾何学を「ユークリッド幾何学」と呼び、曲がった面上で成立する幾何学が「リーマン幾何学」なのだ。つまり「リーマン幾何学」は「ユークリッド幾何学」を含む拡張された幾何学なのである。「リーマン幾何学」のなかで、平らな空間のみを扱うのが「ユークリッド幾何学」ということができる。
さて、要のテンソル解析なしで一般相対論を語ろうとすると、実はとても難しい。というよりも、テンソル解析を用いたリーマン幾何学を一生懸命勉強させて、最後に、「だからアインシュタインのふたつの方程式は簡単に導かれます。」という結論を押しけられるのが、私の経験した一般相対論だった。
しかし一般相対論とは、そういうものなのだろうか? 数学的技術を持ったものだけが理解でき、その他の人は門前払いではなんか変だ。そう、アインシュタインは、先に一般相対論を着想し、それを記述するのに便利な道具として「リーマン幾何学」を採用したのではなかったか。
これから私は、そのような立場で一般相対論の話をする。従って数学的に厳密には間違ったことを比喩として言うかもしれない。しかし意図的に嘘をつくつもりはないので、それを了解の上、この話を聞いてほしい。一般相対論のエッセンスを理解できれば、視野は広がる。だが、空想の世界をさまよう恐れも充分にある。(但し、一般相対論をちょっとくらい間違って解釈をしても、あなたの人生に影響する要素は極めて少ない。決して間違った人生観を持たないように!)
さて、アインシュタインが導いた一般相対論の結論である二つの式を以下に書いてみよう。
【測地線の方程式】(宇宙時空間の最短距離の方程式) \begin{eqnarray} \frac{d^2x^\mu}{ds^2}=-\Gamma~^\mu_{\alpha~\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds} \end{eqnarray} 【重力場の方程式】(質量が空間を曲げる量に関する方程式) \begin{eqnarray} R^{\mu~\nu}-\frac{1}{2}g^{\mu~\nu}\bf{R}=\frac{8\pi~G}{c^4}T^{\mu~\nu} \end{eqnarray} この2方程式の解が一般相対論の結果である。この式は、数学的には、「連立偏微分非線形方程式」と呼ばれる。逃げ出したくなったであろう。当然であるが、あわてないで。
これが、「テンソル解析という微分幾何学」なのである。が、実は、これを説明しろと言われたら、私も多分下書きだけで三年はかかると思われるで、私の能力範囲を完璧に超えている。
説明の下書きだけで三年かかるのだから、この方程式を解くとなると、多分私の一生を費やしても追いつかないであろう。
現実に、昔は、この方程式を解くことに一生を費やした人もいるのだ。今は、コンピュータというものがあるので、数値計算というものをコンピュータにやらせようとする訳だが、この方程式に与えるべき初期条件が自明でないので、様々な解が出てきてしまう。
こんなもの説明できるか、というわけで、特殊相対論を説明してきた、初心者にもわかる、というキャッチフレーズは、一般相対論では、捨てなければならない。それとも三年待ってまで、上の方程式を理解したい?
ここは、なにがなんでも、上の方程式は忘れてもらわねばならない。しかし書いてしまった...
(上の方程式に対する質問は、一切無視するので、そのつもりで。)
一言いいたい!

【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
4.改めて二つの原理
前回書いた方程式が頭から離れないあなた。忠告する。深入りしてはだめだ。「理解の泥沼」にはまる、大学時代に自らそれを体験した私が言うのだから間違いない。
但し、これだけは言っておかなければならない。アインシュタインは、物理現象を幾何学で表現しようとした、ということである。
幾何学、要するに、絵を描いて、補助線を引いて、証明する、あの幾何学だ。これは、加速系も重力系も、幾何学で表現したということだ。
これは何を意味するのか、結論を言っておく。
(4次元)時空間における、物体運動の物理法則は、時空間の曲がりとして表現できる。ということである。
加速系も重力系もひっくるめた、いわゆる一般の非慣性系は、「時空の曲がり」として記述できる。
これが重要である。そして、その結論(アインシュタインの二つの方程式)は、みごとにそれを実現しており、そう考えることに整合性があることを示唆している。
アインシュタインが、一般相対論で目指したのは、重力と慣性力を区別せず、時空間の曲がりとして捉えようとしたことであり、テンソル解析という数学は、アインシュタインが、宇宙を絵に描こうとした筆だと思ってもらいた。なに? やけに重い筆だって? 当然、「重力」の話だもの。
あの方程式は忘れても、一般相対論の枠組みは話す事ができる。安心してほしい。
(第1原理)この二つの原理が一般祖対論のバックボーンとなる。
「重力」と「慣性力」は区別できない・・・等価原理
(第2原理)
物理法則は、宇宙のいかなる系においても成り立つ・・・一般相対性原理
第1原理については、第2項の図15-1と図15-2を見返してもらえば、これは了解してもらえるはずである。
第2原理は、これまで述べてきたように、いかなる運動をする物体にも適用できる物理法則が存在する、ということである。
「特殊相対性原理」が、この宇宙に絶対静止系は存在しない、という重大なことを言っていたのを思い出して欲しい。
一般相対性原理は何を言っているのだろか、と考えてみる。
アインシュタインが時空を記述するのみ持ち出した二つの方程式をもう一度書く。
【測地線の方程式】(宇宙時空間の最短距離の方程式) \begin{eqnarray} \frac{d^2x^\mu}{ds^2}=-\Gamma~^\mu_{\alpha~\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds} \end{eqnarray} 【重力場の方程式】(質量が空間を曲げる量に関する方程式) \begin{eqnarray} R^{\mu~\nu}-\frac{1}{2}g^{\mu~\nu}\bf{R}=\frac{8\pi~G}{c^4}T^{\mu~\nu} \end{eqnarray} 【測地線の方程式】が導くものは、時空の最短距離である。これは、あらゆる物体は、(力が働かなければ)時空の最短距離を移動する、ということを数式化している。
そして、【重力場の方程式】は、物質が時空を曲げる量を数式化したものである。
これらの方程式に、光を当てはめてみると、次のことが言えるのである。
光は、この宇宙をかならず最短・最速で走る最短については、どんな物体も(力が働かなければ)最短の経路を走るので、それほど重要ではない。問題は、最速である。特殊相対論では、光速は不変であり、かつこの宇宙の最速であった。
一般相対論では、「光速は不変である」とは言っていない。だが、最速である、という事実は変わらない。というよりも光はこの宇宙の最短コースを、他の物質に対し最速でしか走れない、ということだ。
何をあたりまえのことを言っているのだと思った人に言っておく。アインシュタインは、光も時空の曲がりに沿ってしか走れない。即ち「光も曲がる」ということを予言した。
えっ、言ってることが矛盾してるんじゃないか、と思う方、考えてほしい。曲がっていても最短・最速であるケースを。
一言いいたい!

【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
5.曲がった時空間
前項の宿題、考えてみた?
そう、曲がっているのに最短コースの話。
まず答えを言ってしまおう。
地球で例える。(地球表面は、あくまで2次元の面ではあるが、)経線(南極と北極を結ぶ線)は常に地球上での最短コース(大円という)だが、緯度線(赤道で大円となり、極で点になる)は、赤道以外は全て最短コースにならない。これはわかると思う。
よく御承知の世界地図(メルカトル図法が多い)で、飛行機や船の経路線、例えば、東京とロサンゼルス間を結ぶ線が上向きにカーブしているのを見たことはないだろうか?あれは、実は遠回りをしているのではなく最短コースを飛んでいる。あの線が、地球上では大円になるのである。
地球上は、球面であり平面ではない。これを無理矢理平面の地図にするから、上記のような錯覚を生ずる。
さて、同じように空間も平空間(こんな言葉はないよ!)でなく曲がっていたらどうなるか? おそらく真っ直ぐに引いたはずの線が曲がって見えるであろう、と想像できる。
真っ直ぐに引いた線とは何か?曲がった空間に引いた最短・最速コースが「光子」の軌跡である。ただし、これを直線とは呼ばず、「測地線」という。この宇宙の曲がりは、平面と比べた球面のように、どこもかしこも一定の曲がりではない。従って、局所的に大きく曲がった場所を割と平らなところから眺めてやると、かなり曲がって見えるのである。しかも(!)アインシュタインは空間だけがまがっているのではなく、特殊相対論同様、「時間」も曲がっている、と言ったのである。
アインシュタインはそれを、「光」であるとしたのである。
うーむ、空間の曲がりまでは、なんとなくわからないなりに、わかったような気がしろ、と言われれば、納得してやってもいいが、時間が曲がるっちゅうのは、どう想像すればいいのだ? と思う人、今からそれをわかりやすく説明する。
まず時空間の曲がりは、局所的である、ということ。つまりまんべんなくのっぺりと曲がっているのではなく、曲がりとは、その場所場所が持っている性質である、と、とりあえず考えてもらいたい。
そうすると、極々小さな範囲には、特殊相対論が適用できるのである。というか、それ故に「光」が登場する。特殊相対論は、空間に時間を仲間にいれた「四元物理量」を元に展開された。従ってそれを拡張した一般相対論にも時空間が関わるのだ。
特殊相対論が、電磁波(光)を扱った理論であるのに対し、一般相対論は、重力を扱うので、全く違って見えるが、実は繋がっているのである。
アインシュタインは、「物理現象を幾何学で表現しようとした」と、前項で書いた。すなわちこれが、曲がった時空間だ。一般相対論では、その時空間の曲がりを表現するのに「リーマン幾何学」(すなわちテンソル解析)を用いたので、数学的には「一般」という名とは裏腹に、一般の人にはわかりにくい理論になってしまったが、実は、その概念はそれほど難しくない。
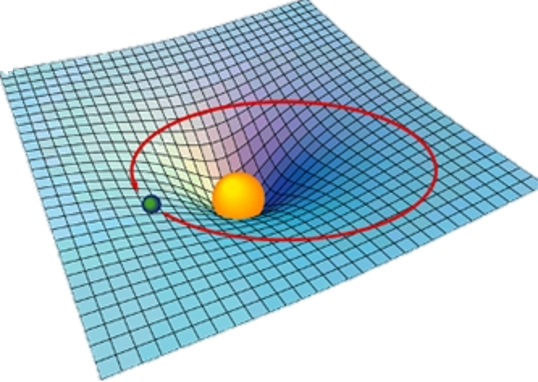
この宇宙では、質量が存在する場所(あるいは、物体が加速により力を受ける場所)では、時空間が曲がるのだ。空間的には、トランポリンの上に砲丸をおいた、あのへっこんだ図を頭に思い浮かべてみて、それが、時間にも及ぶと考える。そこに近づいたビー玉は、そのへっこんだところに落ちる。
簡単に言うと、質量在るところに引力在りということだ。
そして、光もその空間の曲がりに対して、「落ちる」のである。これが一般相対論の答え(時空間での事実)である。
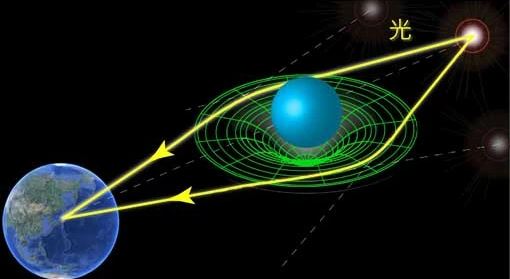
光が曲がっている上図を見て貰いたい。これを、時空の曲がりが少ない(比較的平らな)時空から見れば、自分のいる場所より光は余計に走るから、光は自分の系の光速より遅く観測されるはずだ。
驚いたでしょう。
「光速度不変の原理」はどうした!と叫ぶあなた、そうあなた、あなたは正しい。非慣性系においても、光速度は不変なのである。前に言ったはずである、「光速度不変」は、慣性系に限らない、と。
なにを言っとるんだ、血迷ったか!と思わないでもらいたい。光速度が遅く見えるのに、光速度不変を主張すれば、当然、曲がった時空では、時計が遅れるのである。だから光速度は不変なのだ。
一言いいたい!

【わかっても相対論 第5章 一般相対性理論】
目次へ 次へ進む 前へ戻る
6.一般相対論の世界
光速度不変は、一般相対論でも通用すると言った。だが、特殊相対論とは、一味も二味も違う。
曲がった時空間というのは、便宜的に考え出された抽象的概念ではなく、数学的な裏付けもある現実だ。ということだ。
だから、その曲がった時空間を運動する物体及び光は、その曲がった時空間に逆らわず動いている限り、何の力も感じない、つまり慣性系と同様に扱える、ということだ。
だから、曲がった時空間に沿って測地線上(最短距離)を走る光は、光速度で走る。それを、曲がりの異なる時空間から見れば、光速度ですら変わる。これが一般相対論だ。
そして、等価原理から、それは、重力が働く系だけではなく、加速している系でも、全く同じだというのである。
ロケットの図を思い出してもらいたい。地球上での重力による加速度は、$9.8m/秒^2$である。(ガリレオが、実験で、それを求めた。)
地上に立っているロケットの下には、膨大な質量を持つ地球があって、その結果、物体は、$9.8m/秒^2$という加速度で落下する。
ところが、$9.8m/秒^2$という加速度で宇宙を航行するロケットの内部では、その後方に地球があるのと全く同じ現象しか観測できないと言うのだ。
これはどうしたことだろう。地球という質量を、もしエネルギーに換えれば、とんでもない膨大なものになるのは、($E=mc^2$)の説明で述べた通りだ。ところが、たかが、$9.8m/秒^2$で加速するロケットにとっては、そのような膨大なエネルギーが自分の後方にあることと区別できないと言うのだ。
勘違いしてはいけない。地球をまるごとエネルギーに換えてしまえば、そこから発せられるエネルギーは、ロケットを、$9.8m/秒^2$程度の加速度で動かすどころではない状態にしてしまう。動かすどころではない。ロケットそのもを蒸発させることだろう。
地球という物質が、空間を曲げる量が、ロケットが、$9.8m/秒^2$で加速しているときの空間の曲がりと同一だと言っているのである。勘違いしないように。
【本章の参考文献】
松浦壮著
「時間とは何だろう」 講談社 BLUE BACKS
次章へ 一言いいたい!
