【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

１．疑問はないか

この章は、前章「はじめに光速度ありき」の補足である。

ただし、前章を読んで何の疑問も持たなかった人は、この章を読み飛ばしてかまわない。ここを読まずに先へ行っても何の問題もない。

「４次元のピタゴラスの定理」が本当に自明なのか、という疑いが芽生え、放置できなくなった方に限り、この章をじっくり読んでいただきたい。
（賢明なる読者諸氏は疑問を持ったことだろうなぁ。。。）

前章で述べたように、「３次元のピタゴラスの定理」は、３次元空間に存在する私たちにとっては極めて自明な定理である。ある長さを持った棒は、この宇宙のどこに持って行っても同じ長さである、ということを式で示したにすぎない。

しかし「４次元のピタゴラスの定理」はどうだろうか。前章で私は、時間を含めた事象の隔たりが不変量になる、と書いた。３次元では棒の両端が「隔たり」であり不変量を表すなら、４次元では時間が加わったぶん、出来事の「隔たり」が不変量だと、私は言いくるめたかったのである。

しかし読者諸氏としては、ここは大いに不満を持って然るべきところである。昨日の東京の出来事と一昨日の大阪の出来事の隔たりは、この４次元時空のどこに持って行っても同じである、という主張を自明の理として認められる人がいたら、逆に私は驚くだろう。

前章で私は次のように書いた。

ところが、点Ａ点Ｂ共に、原点から光が走った距離は \begin{eqnarray} x_1^2 + y_1^2 + z_1^2 = (ct_1)^2 \tag{1}\\ x_2^2 + y_2^2 + z_2^2 = (ct_2)^2 \tag{2} \end{eqnarray} ということになる。
（中略）
つまり、４次元時空間では、時間を含めた事象の隔たりが不変量になるのである。よって３次元のピタゴラスの定理から、これを４次元時空間に応用して \[(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 - (ct_2 - ct_2)^2 = S^2\] と表すことができる。

ここを読んで、みなさんは、次の疑問を持ったはずである。
ここから言えるのは、 \begin{eqnarray} x_1^2 + y_1^2 + z_1^2 - (ct_1)^2 = 0 \\ x_2^2 + y_2^2 + z_2^2 - (ct_2)^2 = 0 \end{eqnarray} ということだけではないのか？

正にその通りで、実はこの式は、光（と同じ速さで走るもの）にしか成立しないものなのである。

正直に白状すれば、私は前章で大事な説明をすっ飛ばしたのである。ただし、それには理由がある。この説明を始めるとちょっと時間がかかる上に少なからず数式が登場するのである。読み進める上で躓きになると判断して書かなかったのだが、この疑問を放置したまま「わかっても相対論」を完結させるわけには行かない。
ということで、私はこの章では、以下の２点を語る。

（１）ローレンツ変換の意味
（２）４次元のピタゴラスの定理が示すもの

少々長くなるがお許しいただきたい。ただ、この項を制覇すれば、皆さんは、特殊相対論については理解できたと思っていただいてかまわない。


一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

２．座標変換

「座標」とは、（幾何学では）ある特定の点を指定するための数値の組をいう。１次元ならば、それは原点からの長さ$(x)$であり、２次元ならば、幅$(y)$が加わり二つの数値の組、３次元ならば、更にプラス高さ$(z)$と、三つの組になる。図５を見てもらえれば、これは納得してもらえるだろう。

しかしながら、「座標」の書き方は一種類ではないのである。

図５は、小学校からお馴染みの直交座標なのだが、図６は、サイン($sin$)やコサイン($cos$)を勉強する時に出てくる極座標というものであり、原点からの距離($r$)で表される直線と、その直線と二つの座標軸との角度$(\phi,\theta)$という３組の数値で表されるものである。




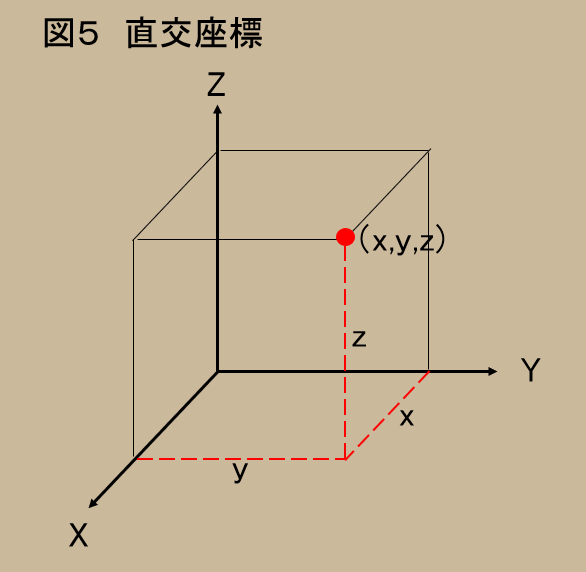
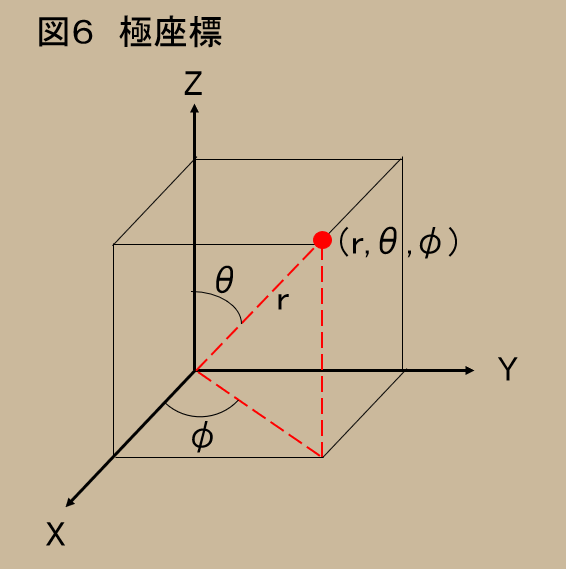
いずれにしろ、どんな座標を選んでも、２次元ならば２個、３次元ならば３個の数字の組で、場所が決定される。一般にはｎ次元では、ｎ個の数値を持ってくれば、座標上の点を確定することができるのである。
というよりも（幾何学では）ｎ個の数値で、ある一点を決定できるところを、ｎ次元空間と定義する、というのが正しい。
従って４次元時空では、４つの数字の組が必要になる。

さらに、例えば同じ直交座標を用いていても、複数の座標が、互いに回転したり、原点が異なったり、ある相対速度で動いていたりする場合もある。そうなると、それらの座標について、それぞれ、自分の座標の数値を用いて、相手の座標を示してやらないと何かと不便なだけでなく、混乱するだろう。自分の座標と相手の座標との関係を示してやる手段を座標変換という。

ここでは、慣性系にある二つの直交座標を使い、その座標が相対速度を持って運動している場合の座標変換を考える。（相対論の話をしているのでこの変換を選ぶのは納得してもらえると思う。）
また、この後の記述では、物体は$x$軸方向のみに移動するものとし、空間における$y$と$z$は変化しないものとして省略する。（省略するのは、何かをごまかそうとしているのではなく、単に同じ記述が三回現れる煩雑さを回避するためと考えていただきたい。）
そうすると、例えば光が走る様をグラフに書くと、図７のようになる。


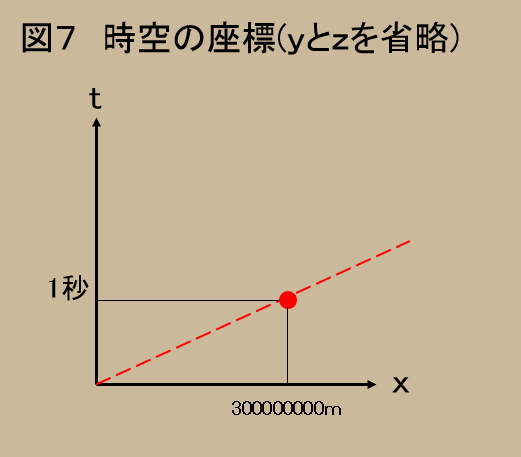
光は(空間では)$x$軸に沿って光速($30$万$km/$秒$=300000000m/$秒)で走るから、時刻$0$秒に発した光は$1$秒後に$300000000m$先へ届く。
しかしながら、横軸は距離($m$)、縦軸は時間(秒)で単位が異なる上、相対論は光の速さを扱うので、$1秒$に対して$3$億$m$というようなバランスの悪いグラフになってしまう。

そこで、どちらの軸も距離になるように工夫をする。つまり図８のように縦軸を時間($t$)に光速($c$)を掛けた($ct$)で表現してやるのである。


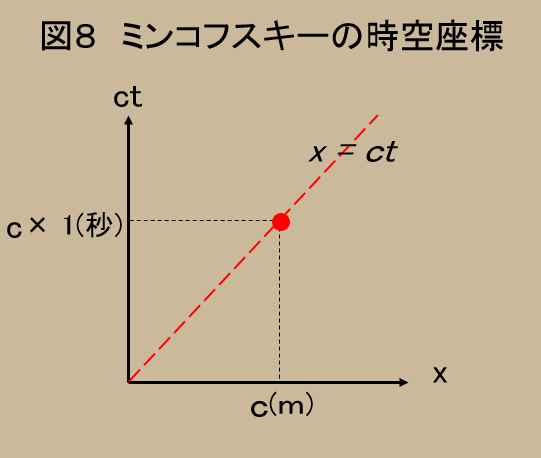
すると、縦軸は、$1$(秒)で光が走る距離$c$($m$)を示し、横軸は7図と同じ$c$($m$)となるので、光の軌跡は傾き45度の綺麗なグラフ($x=ct$)を描く。この縦軸に($ct$)を採用する座標を、考案者の名を取って「ミンコフスキー時空座標」という。

実は、前章で出てきた位置の四元量($x,y,z,ct$)というのは、このミンコフスキー時空座標における数値の組なのである。

この段階では、この時空座標のありがたみはまだ理解できないだろうが、時間軸に($ct$)を採用する利点は読んで行けばわかるように書くつもりである。


一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

３．ガリレイ変換

前項で出てきたばかりなのに申し訳ないが、一旦、ミンコフスキー時空座標から離れる。

今、慣性系Ｑを便宜的に静止しているとする。このＱに対し速度 $v$ で$x$軸方向に走っている慣性系をＲとする。この両座標系にとって同一の事件を、それぞれ、($x,t$)、($x',t'$)と表す。

さらに、この両座標は、$(x,t)=(0,0)$のとき、$(x',t')=(0,0)$となるように原点が一致していたものとする。すると慣性系Ｑにとって（t）秒後、慣性系Ｒにとって（t'）秒後を図で示すと図９のようになる。


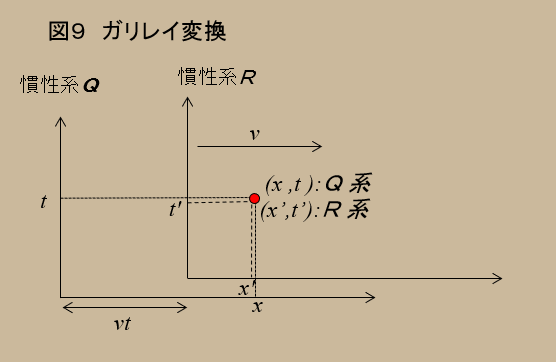
相対論が世に出るまで（いわゆるニュートン力学）は、この間の座標変換、つまりＲ 系の座標をＱ系の座標数値で表す式を \begin{eqnarray} x' &=& x - vt \tag{1}\\ t' &=& t \tag{2} \end{eqnarray} と表現した。
図９を見ていただきたい。Ｑ系が（便宜的に）静止していて、Ｒ系が右へ速度$v$で動いている。
ある点を考える。Ｑ系では$(x,t)$、Ｒ系では$(x',t')$で示される点である。（この点は同一の出来事を表している）
$x'$は、$x$から（$vt$）を引いたものであることは、見たとおりである。そして、経過する時間は、Ｑ系でもＲ系でも変わらない。従って、(1)式、(2)式が導かれる。

但し、ニュートンは、(2)式については明示していない。それは、Ｑ系とＲ系で時間が異なるなどという発想そのものが概念として誰の頭にも存在していなかったからだ。

常識的にはこれで納得のはずである。相手が、いつどこにいてもこの変換式で相手の座標を自分の座標で書き表すことができる。この変換式を、「ガリレイ変換」と呼ぶ。（なぜかニュートン変換ではないのだなぁ。）

(1)式で、３次元空間における棒の長さを考えてみる。
Ｑ系における棒の両端を、$A(x_1,t)$、$B(x_2,t)$とすると、同じ棒をＲ系では$A'(x'_1,t)$、$B'(x'_2,t)$と見るから、棒の長さは、Ｑ系では$(x_2 - x_1)$、Ｒ系では$(x'_2 - x'_1)$で表される。
ダッシュ付きをダッシュなしに置き換えると、$(x_2 - vt) - (x_1 - vt) = (x_2 - x_1)$となり、結局は、Ｑ系でもＲ系でも同じになる。

ガリレイ変換においては、(1)式も(2)式も空間$(x、x')$と時間$(t、t')$の双方に係数がついていない。従ってどちらから見ても、相手の長さ、時間は伸び縮みすることはない。時間的には全く同一、空間的には相対速度に対応して互いの距離が変化するのみである。

このように、ガリレイ変換では、相対速度を持った慣性系では、時間(時刻の差)、空間(物体の長さ)は、どちらからどちらを見ても変化しない。いかなる慣性系でも、別の慣性系を見た時、相手の時間、空間(長さ)は不変なので、これを「絶対時間」「絶対空間」と呼ぶのである。


一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

４．ローレンツ変換

ところが相対論の出現によって、相対速度を持つ慣性系の間の時間は同じには進まないし、相手の長さも変わることがわかった。だから、ガリレイ変換の時間、空間に係数を導入して一般化しなければならなくなった。
ガリレイ変換を一般化して書くと次のようになる。 \begin{eqnarray} x' &=& A(x - vt) \tag{但し $A=1$}\\ t' &=& Bx + Dt \tag{但し $B=0,D=1$} \end{eqnarray} ここで出た係数$(A,B,D)$を改めて求めてみるのである。もし、$(A=1,B=0,D=1)$となるのであれば、この宇宙はガリレイ変換の通用する場所ということになる。
(係数に、文字$C$を使わなかったのは、光速度の記号($c$)と紛らわしいからで、特に意味はない。)

さて改めて、次の式を置く。 \begin{eqnarray} x' &=& A(x - vt) \tag{1}\\ t' &=& Bx + Dt \tag{2} \end{eqnarray} さて、では光速度不変という条件の元で、係数A,B,Dを求めてみよう。
前項で次の式が出てきたことを思い出してほしい。(それぞれの系での球面の式である。) \begin{eqnarray} x^2 + y^2 + z^2 &=& (ct)^2 \\ x'^2 + y'^2 + z'^2 &=& (ct')^2 \end{eqnarray} 光速が不変なので、異なる慣性系（ＲとＱ)でこれが成立する。今は、$y$と$z$を省略しているので
\begin{eqnarray} x^2 &=& (ct)^2 \tag{3}\\ x'^2 &=& (ct')^2 \tag{4} \end{eqnarray} を考えればいい。

(4)式に(1)(2)式を代入する。 \begin{eqnarray} &A^2&(x - vt)^2 = c^2(Bx + Dt)^2 \\ &A^2&(x^2 - 2vxt + v^2t^2) = c^2(B^2x^2 + 2BDxt + D^2t^2) \\ (&A^2& - c^2B^2)x^2 = (c^2D^2 - A^2v^2)t^2 + (2c^2BD + 2A^2v)xt \end{eqnarray} これを(3)式と比較すれば、 \begin{eqnarray} A^2 - c^2B^2 &=& 1 \\ c^2D^2 - A^2v^2 &=& c^2 \\ 2c^2BD + 2A^2v &=& 0 \end{eqnarray} という連立方程式が出てくる($A､B､D$の三つを求める三元連立方程式)。解き方の詳細は省力するが、 \begin{eqnarray} A = D = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \\ \\ B = \frac{-\frac{v}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}} \end{eqnarray} が得られる。つまり、光速度不変という条件下では、ガリレイ変換$(A=1,B=0,D=1)$は成立しないことが判明した。これを(1)(2)式に戻すと \begin{eqnarray} x' = \frac{x - vt}{\sqrt{1 - \frac{v^2}{c^2}}} \tag{5}\\ \\ t' = \frac{-\frac{v}{c^2}x+t}{\sqrt{1 - \frac{v^2}{c^2}}}\tag{6} \end{eqnarray} となる。
(5)式を空間のローレンツ変換、(6)式を時間のローレンツ変換というのである。

複雑に見えるかもしれないが、この変換を使えば、光速度不変という条件下で相手の座標を自分の座標で書けるのである。相対速度（$v$）が光速（$c$）より非常に小さければ、この二つの式がガリレイ変換に近づくことは容易に見てとれるだろう。（つまりガリレイ変換とは、相対速度が光速度に対し、無視できるほど小さい場合の近似だったのである。）

さて、これから手品をご披露する。だまされないようによく見ていてもらいたい。

まず、ローレンツ因子を($\gamma$：ギリシャ文字のガンマ)と書く。（そろそろお馴染みになったはず。） \begin{eqnarray} \gamma ~= \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \end{eqnarray} するとローレンツ変換は次のようになる。 \begin{eqnarray} x' &=& \gamma ~(x - vt) \tag{5'}\\ t' &=& \gamma ~(-\frac{v}{c^2}x+t) \tag{6'} \end{eqnarray} 次に、光が走る距離($ct$)を($w$)という文字で書けば \begin{eqnarray} x' &=& \gamma ~(x - \frac{v}{c}w) \\ w'/c &=& \gamma ~(-\frac{v}{c^2}x + \frac{w}{c}) ~ → ~ w' = \gamma ~(-\frac{v}{c}x + w) \end{eqnarray} 更に、$(v/c)$を($\beta$)と書いてしまうと \begin{eqnarray} x' &=& \gamma ~( &x& &-& {\beta}&w&) \tag{5''}\\ w' &=& \gamma ~(-{\beta}&x& &+& &w&) \tag{6''} \end{eqnarray} となる。

見ていただきたい、$(5'')(6'')$式の美しさを。
時間と空間の間には、このように綺麗な対称性が現れるのだ。

時間軸に$(ct)=(w)$を採用すると、時間と空間を、このようにシンプルで対称性のある美しい式で書くことができる。ミンコフスキー時空座標の効用である。


一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

５．ローレンツ変換の意味

さて、静止系(便宜的に自分がいる座標系)を直交座標で表したとき、相対速度を持った系（つまりローレンツ変換で求められる系）がどのように見えるか、という話をしよう。

前項では、自分(静止系)に対して相対速度を持った相手の系は、ローレンツ変換で表されることがわかったのであった。

今度は、ローレンツ変換された系が自分つまり直交座標(ガリレイ系)に対してどうなるのかを考えてみるわけである。そのためには相対速度系の座標軸(x'軸、w'軸)を直交座標にプロットしてみればよい。

今度は、ローレンツ変換後の座標を静止系の座標値で書くことが必要なので、ローレンツ逆変換を求めておくことが必要になる。ローレンツ変換は以下であるから \begin{eqnarray} x' &=& \gamma ~( &x& &-& {\beta}&w&) \tag{1}\\ w' &=& \gamma ~(-{\beta}&x& &+& &w&) \tag{2} \end{eqnarray} この逆変換は、 \begin{eqnarray} x &=& \gamma ~( &x'& &+& {\beta}&w'&) \tag{3}\\ w &=& \gamma ~(~{\beta}&x'& &+& &w'&) \tag{4} \end{eqnarray} となる。（難しくないから自分で計算してみてね）

さて、ローレンツ変換後の座標系（これも直線の座標である）にもガリレイ変換と同様に、空間座標（$x'$軸）と時間座標（$w'$軸）がある。

$x'$軸上には、$(1,0)$
$w'$軸上には、$(0,1)$

という点をとって、これをローレンツ逆変換してみる。
→(1)(2)式での計算結果を(3)(4)式に代入すればよい。
\begin{eqnarray} x'&=& 0、w'&=&~0~なら~x&=& 0、&w&=0 \tag{原点}\\ x'&=& 1、w'&=&~0~なら~ x&=& \gamma、&w &= \gamma{\beta} \tag{x軸}\\ x'&=& 0、w'&=&~1~なら~x&=& \gamma{\beta}、&w&= \gamma \tag{w軸} \end{eqnarray} である。
このままではわかりづらいので、具体的に値を決めてみよう。
仮に、($v$)が($c$)の$0.4$倍(相手の相対速度が光速の4割)だとすれば \begin{eqnarray} \beta = \frac{v}{c} = 0.4 = \frac{2}{5} \end{eqnarray} となり \begin{eqnarray} \gamma &=& \frac{1}{\sqrt{1-(\frac{2}{5})^2}} = \frac{1}{\sqrt{\frac{21}{25}}} &=& \frac{5}{\sqrt{21}}\\ \\ \gamma{\beta} &=& \frac{5}{\sqrt{21}}・\frac{2}{5} &=& \frac{2}{\sqrt{21}} \end{eqnarray} となるから、

$x'$軸は、直交系での$(\gamma､\gamma{\beta})$=($\frac{5}{\sqrt{21}},\frac{2}{\sqrt{21}}$)と原点を通る。

$w'$軸は、直交系での$(\gamma{\beta}､\gamma)$=($\frac{2}{\sqrt{21}},\frac{5}{\sqrt{21}}$)と原点を通る。

$\frac{5}{\sqrt{21}}\approx~0.91$、$\frac{2}{\sqrt{21}}\approx~0.44$になるので、図10に示すように、

空間については、ローレンツ系で、長さが縮む（$\frac{5}{\sqrt{21}}>1$）
時間については、ローレンツ系で、間延びする（$\frac{2}{\sqrt{21}}<1$） $w'$軸上には、$(0,1)$

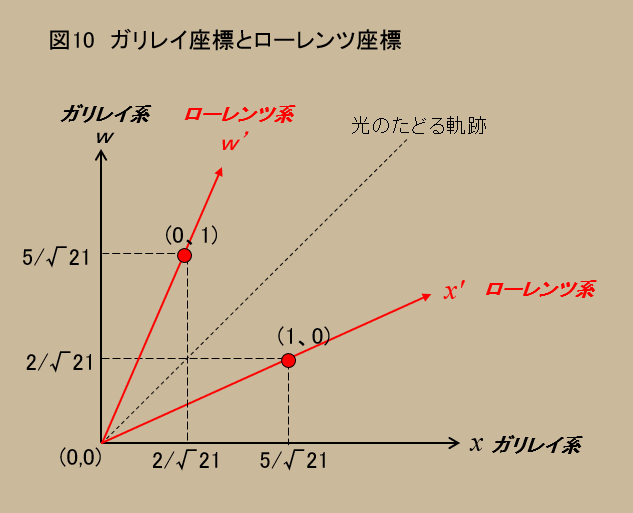
静止系（ガリレイ系）から見ると、相対速度を持って動く系(ローレンツ系)は、斜交座標になることが見て取れる。
ちなみに、相対速度が大きくなるほど座標はより傾き、光の軌跡に近づく。相対速度が光速になると、$x'$軸と$w'$軸は光の軌跡に重なり、時空間が消滅する。


一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】

目次へ　　次へ進む　　前へ戻る

６．時空距離

ここまで延々と数式ばかりで少々お疲れと思う。しかし４次元のピタゴラスの定理を納得してもらうには、ローレンツ変換を説明せざるを得なかったのだ。
ただし、細かいことは忘れてよい。ローレンツ変換の式 \begin{eqnarray} x' &=& \gamma ~( &x& &-& {\beta}&w&)\tag{1}\\ w' &=& \gamma ~(-{\beta}&x& &+& &w&)\tag{2} \end{eqnarray} これだけを、受け入れてもらいたい。
それぞれの式($x'$)と($w'$)を二乗してみよう。 \begin{eqnarray} x'^2 = \gamma^2( x^2 - 2{\beta}wx + \beta^2w^2)\tag{1'}\\ w'^2 = \gamma^2(\beta^2x^2 - 2{\beta}wx + w^2)\tag{2'} \end{eqnarray} ここで$(1')$式から$(2')$式引く。$2{\beta}wx$は相殺され、 \begin{eqnarray} x'^2 − w'^2 = \gamma^2((1−{\beta}^2)x^2 − (1−{\beta}^2)w^2) \end{eqnarray} となる。
ところが$(1−{\beta}^2)$というのは定義から、$\frac{1}{\gamma^2}$なのだから、$\gamma~$も約分されてしまい、結局 \begin{eqnarray} x'^2 − w'^2 = x^2 − w^2\tag{3} \end{eqnarray} が導かれる。
$(3)$式で省略されていたyとzを追加し、$w=ct$を考慮すれば、 \begin{eqnarray} x'^2 + y'^2 + z'^2 - (ct')^2 = x^2 + y^2 + z^2 - (ct)^2 = S^2 \tag{Sは普遍量} \end{eqnarray} が出てきて、私は、ほっとするのである。(４次元のピタゴラスの定理が証明されたのだよ。)

さて、式を眺めてみると、３次元のピタゴラスの定理とは違って、時間の項だけ符号がマイナスになっている。時間の項は時間に光速($c$)を掛けて２乗しているのだから、距離としては非常に大きなものとなる。
皆さんは心配をするだろう。これでは、$S^2$がマイナスになって、$S$そのものが虚数になってしまうのではないかと。
その心配はごもっともなので、４次元のピタゴラスの定理をちょっと変形する。といっても難しいことをするわけではない。式の両辺に(-1)を掛けるだけだ。 \begin{eqnarray} -x'^2 - y'^2 - z'^2 + (ct')^2 &=& -x^2 - y^2 - z^2 + (ct)^2 &=& -S^2 \\ (ct')^2 - (x'^2 + y'^2 + z'^2) &=& (ct)^2 - (x^2 + y^2 + z^2) &=& S'^2 \end{eqnarray} なんのことはない、時空間の時間要素部分と空間要素部分の符号を入れ替えただけだ。$S$にダッシュがついてしまったが、もともと$S$は、不変量として定義したものなので、どんな記号で表そうと問題はない。ここから先では、またダッシュをつけずに$S$で表すことにする。

４次元のピタゴラスの定理を整理しておこう。互いに相対速度を持ついかなる慣性座標系においても \begin{eqnarray} S^2= (ct)^2 - (x^2 + y^2 + z^2) \end{eqnarray} が成立する。（この式では、時間の項($ct$)が一番先に来てしまったので、今後は座標を書くときも、時間を先に持ってくる。）
つまり

時空間に２点、Ａ$(ct_1,x_1,y_1,z_1)$、Ｂ$(ct_2,x_2,y_2,z_2)$を考えると、それをいかなる慣性系からみても、ＡＢ間の距離は$S$という不変量になる

という事だ。そして、この不変量（$S$）を時空距離と呼ぶことにしたのである。
つまり４次元では、このＡＢが時空間における長さの変わらない棒なのである。

アインシュタインが仮定したのは二つ

（１）光速度不変の原理
（２）特殊相対性原理

だけである。

しかし、この二つの原理だけから、相対速度を持つ異なる慣性系間での、相手の時間の遅れ、相手の距離の縮みが導かれ、ローレンツ変換により相手の座標を自分の座標で記述できる。更にローレンツ変換は、時空距離が普遍量であることを証明する。
直感や常識では受け入れることが難しいかもしれないが、光速度が不変で、絶対静止が定義できないこの宇宙では、これが真実なのである。

一言いいたい！





【わかっても相対論　第３章　ローレンツ変換と時空距離】】

目次へ　　次へ進む　　前へ戻る

７．４次元のピタゴラスの定理が示すもの

４次元のピタゴラスの定理は数学的に成立する。それは \begin{eqnarray} S^2= (ct)^2 - (x^2 + y^2 + z^2) \end{eqnarray} である。そういうものと心得よ。
そう言われても、皆さんは、まだもやもやしているかもしれない。

ここまで読んできたことをもう一度振り返ってみれば、確かに（数学的に）間違ったことは書かれていない。それはわかる。しかし、だから時空距離は不変だと言われてもなあ。
そもそも時空距離ってどんなものなんだ？

もやもやは募るばかりだろう。

そこで私は、余計なお世話かもしれないが、この項でもう一言書いておこうと思う。
４次元時空のピタゴラスの定理で、時間の項と空間の項の符号が異なる理由を納得してもらおうと考えるからである。



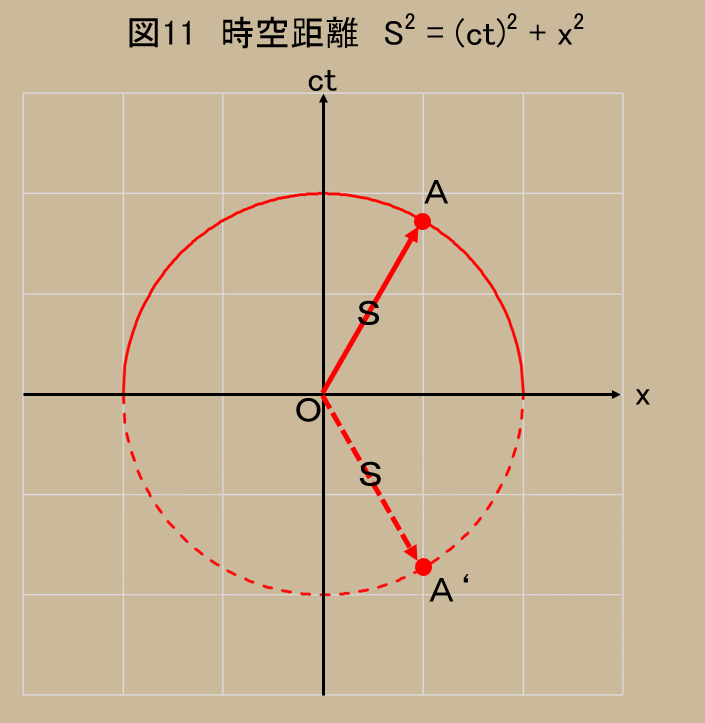
まず、４次元のピタゴラスの定理において、３次元と同じように、時間と空間の項の符号が同じであるとする。図１１を見てもらいたい。（$y$と$z$は例によって省いてある）
あなたは今、点$O$にいるとする。（簡便のため時空座標の原点とした。）
あなたは、そこからある時間をかけて点$A$へ移動した。

そうすると、時空距離（$S$）は、原点を中心とする円となる。
（$S^2= (ct)^2 + x^2$という円の方程式をグラフにしたのだよ。）

つまり、あなたの移動を様々な相対速度を持つ慣性系から見ると、円周上のどこかに達したように見えるということだ。

従って、あなたに対して相対速度を持ったある人には、あなたが$A'$にいるように見えることもあり得る。しかし、これはまずいことになった。

なぜって、その人にとっては、あなたの移動前と移動後の時間が逆転している。

仮に、点$O$であなたが拳銃を発射し、点$A$に弾丸が届き、的（例えばスイカ）を破壊したと考える。（あなた自身が移動するのでなく、弾丸が移動することにした訳だ。）あなたにとっては、この順序に何も問題はない。しかし、あなたに対し、ある相対速度を持った人には、弾丸がスイカを打ち砕いたあとに、あなたの手元の銃から弾丸が発射されることになる。

事象の順序が見る人によって異なる、これはあり得ない。あなたが弾丸を発射するからスイカは砕けるのである。その逆はない。
よって、$S^2= (ct)^2 + (x^2 + y^2 + z^2)$という式は、４次元の時空距離を示すにはふさわしくないことになる。少し、難しい言葉で言うと、この式は、因果律を守れないのである。


次は、時間と空間の符号が異なる式、$S^2= (ct)^2 - x^2$ を見てみよう。



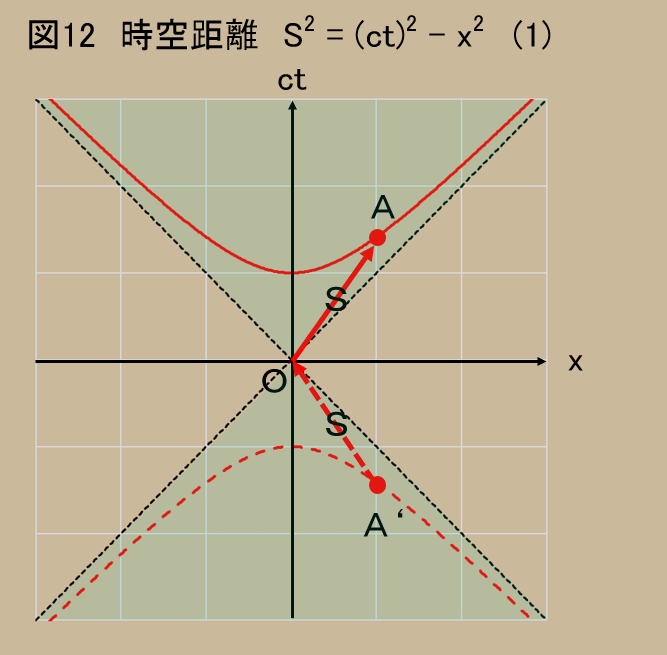
符号が異なる場合、グラフは、円ではなく双曲線を描く。そして、その双曲線は全部で４本描けるのだが、二つに分けて説明する。（理由があるんだ）

まず、図１２である。双曲線は２本ある。
さきほどと同様に、あなたが、点$O$で拳銃を撃ち、点$A$でスイカが砕けると見る。あなたに対して相対速度を持った人は、上側の双曲線上の点で、スイカが砕けたと見るから、全てその事象は点$O$より時間的に後である。因果律を破ることはない。

それじゃあ、下側の点$A'$はどうなのか、と思うよね。
下側の双曲線は、点$O$にいるあなたにとって、全て過去の出来事である。そうだよね。従って、点$O$であなたが弾丸を発射し、点$A'$でスイカに当てることはできない。見るとすれば、あなたが下側の双曲線上にいて銃を撃ち、点$O$でスイカを砕くということはあり得ても、その逆はない。こちらも因果律は守られる。

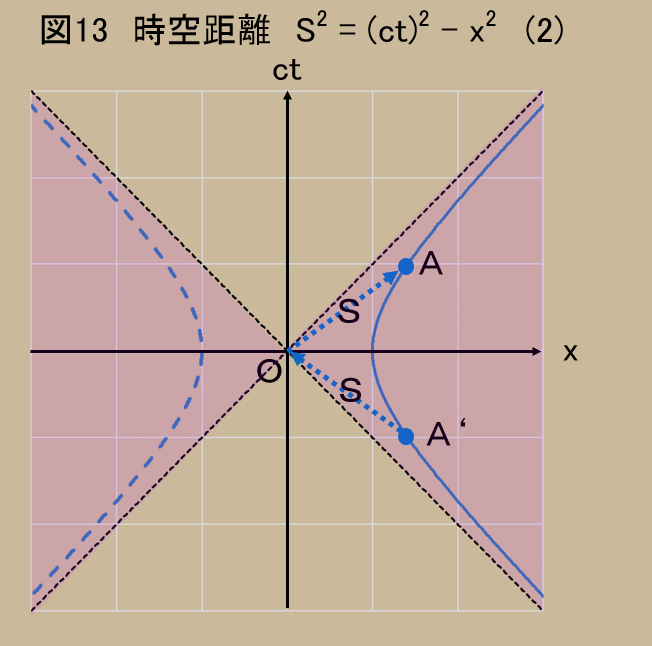
問題は図１３である。円の時と同じように、双曲線は$x$軸を横切って（縦切ってというべきか）いる。これは因果律を破るかもしれない。
確かに、点$A$と点$A'$は同じ双曲線上にあり、時間が逆転している。まずいではないか。

大丈夫なのである。図１３で、点$O$から点$A$までの線が点線で書かれていることに気づいてほしいわけである。実は、点$O$を発したものが点$A$へ到達すること自体があり得ないからだ。
図１２と図１３を別に書いた理由もそこにある。

点$O$に存在するものは、図１２の緑色で塗った部分としか関わりを持てないのである。

なぜか。実は緑の領域の縁（ふち）が光が走る線になる。
グラフの縦軸が、$ct$ なのだから、当然と言えば当然だ。時間距離と空間距離が同じになるのが光の軌跡なのだ。だから光よりも空間を走る速度が遅いものは、全て緑の領域にしか進めない。

事象が原因から結果へ進むという因果律を守るためには、光がグラフの$45$度の線を走り、いかなる相対速度を持つ座標系から見ても一定速度で、かつ最速である必要がある。
「光速度不変」は、実測から仮定された原理であるが、時空距離がいかなる慣性系からも同じになるためには必然であることが、これでわかるのである。

図１３で示される、赤の領域は、点$O$とは、過去・未来にわたり、いっさい関係を持つことができない領域なのである。光より速く走るものしかそこへ踏み入ることができないからだ。絶対に関わることができないところにある事象とは、そもそも因果律というものが意味を持たない。だから双曲線が$x$軸を横切っても問題ないのである。

さて、そういう認識で、改めて図１４をみて欲しい。（図１２の上の部分だ）
少し想定を変える。あなたは、空間上では原点$O$に立ち止まって動かないものとする。しかし、立ち止まっていても時は過ぎさるから、あなたはある時間後には、$ct$軸に沿って、点$A'(ct_0,0)$に到る。

これを、あなたと相対速度を持つ誰かが見れば、動いているのはあなたの方になるのだから、あなたは点$A(ct_1,x_1)$に移動したように見えるはずだ。

このことを少し考えてみよう。


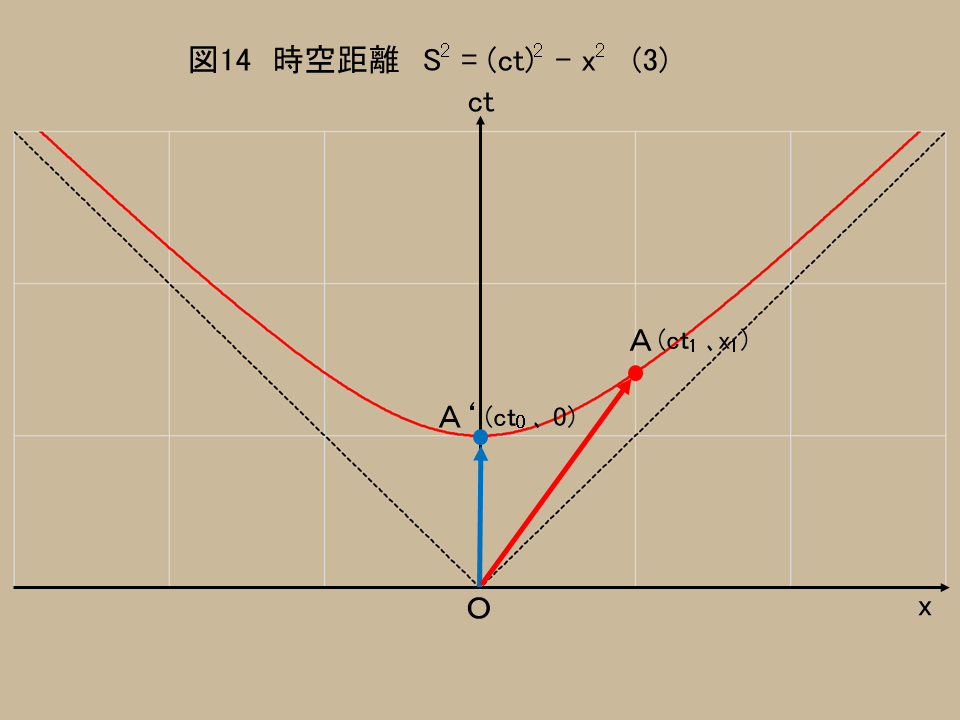
承知の通り、時空間距離を表す式は \begin{eqnarray} S^2 = (ct)^2 - x^2 \tag{0} \end{eqnarray} であるのだから、点$O$から点$A$へ向かうあなたを見る相手の系においては \begin{eqnarray} S^2 = (ct_1)^2 - x_1^2 \tag{1} \end{eqnarray} が成立する。
しかし、空間上を移動せず立ち止まっているあなたにとっては、常に$ct$軸上を動き。$(ct_0,0)$に達することになる。
従って、時空間距離は \begin{eqnarray} S^2 = (ct_0)^2 \tag{2} \end{eqnarray} と表される。
(1)式と(2)式を比べて欲しい。
注意することは、二つの式は、$S^2$という同じ値であることだ。（グラフでは、$OA$と$OA'$の長さが異なるが、惑わされてはいけない。不変になるのは時間距離の2乗から空間距離の2乗を引いたものだ。）

(1)式では、$x_1^2$が引き算されているので、明らかに、$(ct_0)^2 ＞ (ct_1)^2$である。
ということは、時間がプラスである限り、$t_0 ＞ t_1$ となってしまう。
つまり、動く物体は、空間要素分の距離を$S^2$に割かなければならないので、時間要素の距離が減ってしまうことになる。
時空間距離が不変であるような系同士では、自分に対して静止している時計（自分が持っている時計）が最も速く進む。自分に対して相対速度を持つ物体の時計は進み方が遅くなるということだ。
何をいいたいのかわからないかもしれない。整理すると、

�@ある座標に対して静止している物体は、その座標にとって最も時間が早く進む。
�Aある座標に対して相対速度を持つ物体は、空間方向への距離分、時間が遅れる。

自分にとって、相対速度がゼロの物体は、空間方向への移動がないので、時間方向に光速で突っ走ることになる。
この時間方向へ距離を変化させるためには、その物体を自分に対して相対速度を持って走らせてやればよい。相対速度が大きくなるほど、空間移動分の距離で、不変量を稼ぐので時間方向への距離は減る。

そして、仮に物体の相対速度が光速になったらどうなるか。
空間方向への移動距離が、時間方向の移動距離と等しくなって、不変量がゼロとなる。これは都合が悪い。なぜなら、不変量であるはずの時空間距離がなくなってしまうのだから。

よって、普通の物体は、光速では走れない。不変量がなくなってしまうからだ。
光とは、空間方向の移動だけに時空間距離を費やしてしまう特殊な存在なのである。だから光が持つ時計は、全く進まない。

ここまでの議論は、ローレンツ変換で述べたことと、全て一致する。
あらゆる物体は、時間方向へ光速で突っ走っている。そして、どんな慣性系からも光速が一定に観測されるように、時間が伸び縮みするならば、４次元時空のピタゴラス量が不変に保たれるように空間(長さ)も、それに協力しなければならない。

そのようにこの宇宙はできている。

ミンコフスキーは、時間を($ct$)という距離の単位で表した。その意味は、時間とは、四番目の見えない方向への物体の移動距離であることを示し、さらにその移動距離に出てくる光速度($c$)を一定にするように時間と空間が協力して不変量を作るのがこの宇宙のあり方である、と明確化したのである。
\begin{eqnarray} S^2= (ct)^2 - (x^2 + y^2 + z^2) \end{eqnarray} この式は、そのような宇宙へ、私たちの認識を導く道しるべとなっているのである。


【本章の参考文献】
　　ブライアン・コックス、ジェフ・フォーショー著、柴田裕之訳
　　　「なぜ$E=mc^2$なのか？」　紀伊國屋書店

次章へ　 一言いいたい！