【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
1.光電効果:光の持つエネルギー
さて、アインシュタインの登場である。
彗星のように物理学の世界へ登場したアインシュタイン。でも、『アインシュタイン=相対性理論』なのではない。
アインシュタインは、ノーベル物理学賞を受賞しているが、その時の功績は何だったか、ご存じだろうか? こんなことを尋ねるからには、相対論でないことはわかるであろう。実は、「光電効果」がそれである。(アインシュタインが光電効果を論文で発表したのは、1905年のことである。)
アインシュタインの「光電効果」が、日本に紹介された時、某新聞には、「写真電気効果でノーベル賞」と書かれたそうだ。なんだそりゃあ、と思う方、"Photo-Electric-Effect"を訳してみて欲しい。理解できますね。
金属の表面に光をあてると、そこから電子が飛び出して来る現象が「光電効果」である。
これは後々重要な話に繋がるので、少し詳しめに説明しておく。
電子(負電荷)というものは原子核(正電荷)に束縛され、原子核の周りを廻っている。だから勝手に金属から飛び出すことはできない。電子にとって原子核の周りは壁に囲まれた拘置所のようなもので、外から保釈金(エネルギー)を貰わないと壁を飛び越して外に出ることができないのだ。
だから、光電効果とは、電子が光から保釈金(エネルギー)を受け取って、原子の外に飛び出す現象と言うことができる。
光は電磁波という波なのだから、波が運ぶエネルギーをこつこつ受け取って保釈金が貯まったら、原子の外に飛び出すことができる、と当時の物理学者は考えていた。
ところが光電効果を観察してみると、次のような実験結果になってしまった。
(1)波長の長い光(赤外線など)をいくら長時間照射しても、電子は飛び出さない。どうも電子は保釈金をこつこつ貯金することが許されていないようなのだ。なぜなら波長の長い光を長時間照射しても、電子が飛び出さないからだ。
(2)波長がある値より短くなると、ほんの少し照射しても、電子が飛び出す。
ところが、波長の短い光は、瞬間的に、電子に飛び出すエネルギーを与えてしまう。
ちょっと余談
波動において、波長と振動数の関係を説明しておこう。下図を見て欲しい。
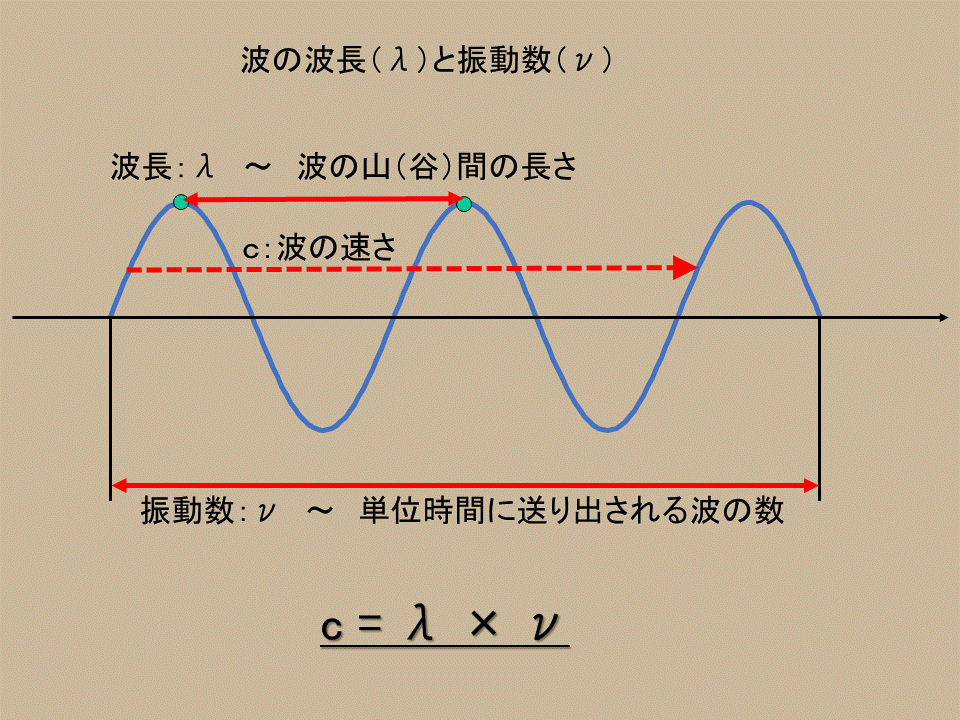
波長($\lambda$)とは、波の山から山(谷から谷)の長さである。そして振動数($\nu$)とは、単位時間に送り出される波の数をいう。
図を見ていただければわかるように、波長(波の長さ)に振動数(単位時間の波の数)を掛けてやると、波の速さ(単位時間に波が進む距離)になる。従って、 \begin{eqnarray} \nu=\frac{c}{\lambda} \end{eqnarray} が言える。
さて、アインシュタインは以上の実験結果から実に斬新なことを言ったのである。
光が波であるなら、光電効果は発生しない。先に述べたように、波長によらず、ある時間光を照射し続ければ、電子に飛び出すエネルギーを与えることができるからだ。
それが成立していないのは、光がエネルギーを持った粒子(のようなもの)であると考えると説明がつく。つまり、光とは波長(振動数)に対応したエネルギーを持った粒の性質をもったものなのだ。波長が短いほど(つまり振動数が大きいほど)、光(の粒)のエネルギーは大きくなる。アインシュタインはこの粒を光量子と呼んだ。後の光子である。
実験結果は、光のエネルギーが、波長に反比例(つまり、振動数に比例)することを示しており \begin{eqnarray} E=h{\nu}\tag{光のエネルギー} \end{eqnarray} と数式化できることが示された。
($h$)は、量子論で重要な意味を持つ定数なのだが、ここでは単なる比例定数だと思っていい。
そして、これが、量子論の始まりにもなっているのだが、後に量子論は不完全であると問題提起したアインシュタインが量子論の黎明期にこんな形で関わっていたことは興味深い。
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
2.コンプトン効果:光の運動量
この項も相対論の観点からは、若干脱線するのであるが、この後の流れには必要なことなので書いておく。やはり量子論に関わることである。
アインシュタインによる光電効果に関する論文は1905年の発表だが、それから18年後の1923年、コンプトンが光電効果の拡張実験を行った。それは、光電効果同様に金属の表面に光を当てるのだが、通常の光ではなく、振動数の大きいX線を照射してみたのだった。この実験でも光電効果同様、金属中から電子が飛び出してきたのだが、同時に照射した$X$線も散乱して出てきた。
ここまでなら、どうということはないのだが、散乱した$X$線の振動数が、照射した$X$線の振動数より小さくなっていることが観察されたのだ。(これをコンプトン効果と呼ぶ)
これは、光が波であったなら、絶対にあり得ない現象であった。これは、光の粒子が、電子に衝突し、その運動量の一部を電子に与え、自らの運動量を減らすというモデルでしか説明できないものだったのだ。
一般的に、波の運動量というものは単純に定義できない。例えば、音波は、人の鼓膜を震わせるのだから、鼓膜に運動量を与えていると考えられるが、これは音波という波の物理量で数式化できるものではなく、ミクロには空気分子の流体力学に関わるものである。そもそも、波は空間に拡がるものであり、特定の場所に存在するものではないのだから、波の運動量というものは存在しないと考えた方がよい。
そもそも運動量とは、物体の(質量)と(速度)を掛けた量として定義されたものだから、波にはこの定義が適用できないのだ。波に速度はあるが、それは進行速度であり、質量の移動速度ではないし、波に質量を考えること自体が不可能だ。
よって、コンプトンの実験による「光の運動量」とは、光を粒子と見なさなければ説明できない。
コンプトンは、この実験結果を子細に検討し、次の結論を得た。
光が電子に与える運動量は、振動数を光速で割ったものに、定数($h$)を掛けたものになる。 \begin{eqnarray} p=\frac{h{\nu}}{c}\tag{光の運動量} \end{eqnarray} 前項で示した \begin{eqnarray} E=h{\nu}\tag{光のエネルギー} \end{eqnarray} と一緒に考えれば、光においては \begin{eqnarray} p=\frac{E}{c} \end{eqnarray} ということが言える。これ、あとで出てくるので記憶の片隅にとどめておいて。
余談
特殊相対論が発表された1905年の時点で、アインシュタインは、(光の運動量)が(光のエネルギー)を(光速)で割ったものであることを示していた。これは、マックスウェルの電磁気学の方程式を検討すると求められるのである。コンプトン効果は、これを実験的に検証したことになる。
話を戻そう。
さて、光は電磁波であり、だから、光という波を伝達する媒体としてエーテルが考えられたのであった。 それが、エネルギーも運動量も持った粒子だって! 人をバカにするんじゃない、と叱られそうだが、アインシュタインは決して、光を粒子だとは言っていない。波長に応じたエネルギーを持つなにか、つまり光量子という「何か」だと言ったのである。 なに、詭弁だって?
そうではない。光が電磁波という波であることは確かなのだが、それとは別に、粒子のような性質も持っていなければならないという事実を述べただけである。この光量子説は、さっきも言ったように量子論に繋がって行くのだが、とりあえずここではこれ以上深入りしない 。
アインシュタインが「光電効果」でノーベル賞を受賞したのは1921年。このとき、相対論は既に世に出ていた。ところが相対論が受賞の対象にならなかったのは、相対論が素直に受入れにくい理論であり、認められるのに20年では足りなかったからだ。
なぜ認められなかったのか? あまりに難しい理論で理解できる人がいなかったからではない。有り体にいうと、相対論から導かれる現象を信じられる人がいなかったからだ。
私見だが、そもそも物理理論を、「信ずる」「信じない」で論ずることに大きな間違いがある。物理学とは、何かを信ずる学問ではない。この宇宙で起こる現象を追求する学問だ。現象を淡々と受け止めるのが物理学である。ならば、この宇宙で起こる事柄を「信ずる」も「信じない」もない。それが起こっているのだから、それを説明する、これが物理学の立場だ。この前提を崩せば、そもそも物理学に意味がなくなる。
物理学者が、もし何かを信ずるとすれば、それは、この宇宙は物理法則に従うということだけであろう。つまり、光が波の性質と粒子の性質の双方を持つのは現象であって、「信じられない」というものではない。同等に、光速を誰が測定しても同じになるのは、物理法則の結果であると見なければならない。
繰り返そう。特殊相対論は、数学的には、微分も積分も必要ない。本当に高校1年程度の素養があればよい。
この際なので、もう一つだけ言っておきたい。
光電効果も相対論もコンプトン効果も、その正当性は確認され続けており、間違いは発見されていない(現実の宇宙との食い違いが見いだされていない)。だからこの理論は生き残っている。
これは、物理学者が、相対論を「信じていない」証である。信じている理論を誰が検証し続けるだろうか。
物理に絶対に正しい理論など存在しない。検証に耐え続ける理論があるだけなのである。
相対論が認められなかったのは、理論が難解だったからではなく、それが導く現象の意味することが常識破りであり、それが、自然をより正確に記述する理論であると、誰も認める勇気を持つことができなかったからである。
まとめておこう。
(1)光は、電磁波という波である。
(2)光は粒子の性質を持っていると考えないと説明できない現象がある。
(3)光は、粒子としてのエネルギーを持っている。
(4)光には、他の粒子と相互作用して、運動量を交換する。
(5)光のエネルギーは、$E=h{\nu}$
(6)光の運動量は、$p=\frac{h{\nu}}{c}=\frac{E}{c}$
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
3.二つの原理
光(=電磁波)は、エーテルを媒質とする波であると考えて、速さを測定してみると、実際の波(音波など)とは異なる結果が得られたことを前章で書いた。
それはエーテルに対して動く観測者が、どのような方向から来る光速度を測っても、その値は同じになるということであった。(マイケルソンとモーリーの実験は、エーテルに対して地球が動いているという前提で、進行方向とそれに垂直な方向での、光の往復時間を計り、それが厳密に一致することを示したのだが、同じことを言い換えると、どのような方向からの光速度も同じ、という結論になる。)
これに対して、ローレンツは、エーテルに逆らって進む物体は、その方向にある値(ローレンツ因子)をかけた分だけ縮むとして、状況を説明したのだった。
ただし、全ての物質がエーテルに対して縮んでしまうので、当然ものさしも縮み、その縮みを絶対に検出できないことも、前章で書いた。
絶対に測定にかからないものを仮定した理論は無意味である(つまり、エーテルは原理的に観測できない)ということから、「エーテルという仮説を捨ててみたら」ということを考えたのが、アインシュタインであった。(アインシュタインは、決してエーテルを否定した訳ではない。エーテルを考えなくとも、実験事実を説明できると考えたのである。)
詳しい話に入る前にひとつだけ整理しておこう。それは、光を波(あるいは粒子)と考えたときの振る舞いが、実際は我々の知っている波(あるいは粒子)と異なるという点である。
しつこいぞっ! と怒らないでね。これ大事なことだから。
まず、光が粒子であるとする。
これは、本当に私たちの常識で考えればよい。ある人が野球のボールを時速$140km$で投げるとする。球場のピッチャーマウンドからボールを投げれば、バックネット裏で測定したボールの速さは$140km/時$である。ところが、ピッチャーが、センター方向からキャッチャーの方へ時速$50km$の車に乗って、マウンド上に来た時、ボールを放ったらどうなるか。そう、バックネット裏では、ピッチャーの投げる速度($140km/時$)と車の速度($50km/時$)を加算した値($190km/時$)を観測する。光に置き換えれば、光源の速さが観測する光の速さに影響することになる。
次に、光を波と考える。
この場合、観測する者にとって、波源(波を発する者)の速さは、観測者に影響しない。何度も言ったように、波は、その媒質に対して一定の速さなのである。しかし、観測する側が、媒質に対して動けば、観測する波の速度は変わる。
ところが現実に光の速さを測定してみると、
光源が動こうが、観測者が動こうが、どんな場合でも、光の速さは一定なのである。これは、光を粒子と考えても、波と考えても、これまでの常識とは相容れない。
わかりやすい例で言う。
光源Aがあって、ここから速さ($c$)で光が出ている。そしてその光源に速さ($v$)で近づく物体Xと、同じ速さ($v$)で離れ行く物体Yがあるとする。みなさんの常識で考えれば、Xにとっては、光の速さは、$(c + v)$であり、Yにとっては、$(c - v)$に見えると思うだろう。(もちろん、Aにとっては $c$ である。)光を波と認識していれば、それで正常である。
また、あなたから見て、光速の$0.8$倍で走っているロケットが、前方に光を発した場合、その光の速度は、あなたにとって、($0.8+1.0=1.8$)つまり光速の$1.8$倍と見える、これは光を粒子と認識した時の常識である。
ところが、どんなケースでも、光の速さは同じ($c$)に観測されるのである。
これは、アインシュタインが言い出したことでも、相対論における結論でもない。観測するとそうなってしまうのである。(つまり、光速度が一定なのは、そもそもの前提になってしまうのだ。ここを勘違いしないように。)
そこで、アインシュタインは考えた。光速度は、どう測っても同じになるのがこの宇宙の性質なのではないか、と。なぜと言われても答えようがない。観測の結果、そういうもんだ、としか言えない。
補足しておくと、マックスウェルの電磁気学において求められる電磁波の速さは、「何に対して」という但し書きが付かない。真空中の電磁波の速さが出てくるだけである。当時一部の人達には、これが理論の綻びに見えたのだが、実は真空中の電磁波は、観測者によらず一定だったのだ。
そこで、アインシュタインは次の原理を提案した。
(1)光の速度は、いかなる慣性系から測定しても同じである。慣性系ってなんだ? 本当はこの原理に、慣性系という言葉はいらないのだ。だったら、はずせ! といわないでね。私はこれから「特殊相対性理論」を説明しようとしている。ここで出てくる「特殊」というのは、慣性系のことなのだ。
慣性系(外部から力が働かない系、つまり等速運動をする系)という条件付きで展開する理論を「特殊相対性理論」と呼ぶ。だから第1原理にも、とりあえず慣性系という言葉を入れておく。
アインシュタインは、実験の結果から、光速度一定の原理を仮定したのである。(くどいようだが言っておく。現在まで、この仮定を覆す実験結果はない。)
余談
このアインシュタインの原理を言い換えると、この宇宙とは、『誰にとっても光を一定速度で走らせるところのものである。』という関係代名詞(英語の復習をしましょうね)でしか言い表せないものとなる。だってそういうものなんだから。
そして、この後、この関係代名詞的な言い方しかできないものが物理学では増えてゆく。
例えば、光とは、波として観測すれば波であり、粒子として観測すれば粒子である、そういうところのものである、という事実がある。これは量子論の結論なのだが、光ってそういうものなのだ。とりあえず相対論には関係ないので詳細は述べないが、そういう言い方をしないと正確に言い表せないものがどんどん出てくる。
閑話休題。
そして、もうひとつの原理を提案した。
(2)どんな慣性系でも、物理現象は同じである。なんぼなんでも、そのくらいわかるわい、あそことここで物理法則が違ったらそもそも物理学なんて意味ないではないか! と怒らないでね。実は、これも大事なのよ。
なんでかと言うと、これは、「全ての慣性系にえこひいきはない」と言っているのだ。なに、まだあたりまえ? じゃあもう少し言い方を変えよう。「ある慣性系のみを特別扱いする理由はない」。
なに、まだ言いたいことがわからん? じゃあもっと噛み砕いてみよう。
「ある慣性系から、別の慣性系を見たとき、そこにあるのは、お互いの相対速度だけである」。
えっ、今度は話が飛躍しすぎてわからない? うーん、そうか。
○時速$200km$で走っている物体(A)がある。自分がどのくらいの速度で走っているのかは、単体では、どの物体もいえないのである。
時速$500km$で走っている物体(B)がある。
(両者とも一直線上にいるものとする。)
といったらおかしいのだ。AとBはいったい何に対して時速$200km$、$500km$なのかを言っていないから。
○そこで物体(C)を持ってきてA及びBは、Cに対して、上記の速度だとする。
(とりあえずCを基準にした)
○そうすると、Cを基準として、BはAにとって時速($500-200)=300km$で
あることしかいえない。
○逆にAもBにとって時速($500-200)=300km$であることしかいえない。
いえるのは、AとBは相対速度、$300km/時$であることだけである。
つまり、第2原理は、宇宙には絶対静止という特別な慣性系を定義できる何物もない、ということをいっている。
複数の物体間には、相対速度があるだけである。この前提を持ってくるので、相対性理論という名称が生まれた。
ところが、この前提とは裏腹に、もうひとつの前提は、光速度は絶対だと主張する。これはおかしいのではないか、だって光と同じ速さで走る者がいたら、そいつは、相対速度を持つのか絶対速度を持つのかわからないではないか。
この疑問に答えるのがこの読み物の目的である。
今回の話をまとめる。アインシュタインは、特殊相対性理論を展開する二つの原理を提唱した。
(1)光速度は、いかなる慣性系から測定しても同じである(光速度不変の原理)ある意味では、特殊相対性理論とはこれだけなのである。これですべてが説明できる。
(2)いかなる慣性系でも、物理現象は同じである(特殊相対性原理)
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
4.思考実験その1(動く時計の遅れ)
物理をかじった人は、よく「思考実験」という言葉を使いたがる。単なる証明(もどき)を「思考実験」にしてしまう輩も多い。しかし、光速度があまりに大きすぎて、日常の現象と全然マッチしないので、相対論では、ときに「思考実験」をしなければならないこともある。
次に示すのは有名な思考実験である。本当に実験すると光速度はえらい大きいので日常生活にあてはめられない。そこで、頭の中で次のようなことを考える(実験する)のである。(くどいが、実際には、本当の実験でも確かめられていますからね。)
【状況】
Yという人がいて、便宜上静止しているとみなす。(全ての慣性系は相対速度しか持たないので、今Y氏を基準系とする。)このY氏の目の前を、(Y氏から見て)右へ速度($v$)で走っている列車がある。列車の中央にはXという人(列車に対して静止)がいる。今、光速度を($c$)で表す。(なぜか光速度は $c$ で表すことになっている。理由を説明したものを読んだことがない。誰か知ってる?)
【X氏が行うこと】
X氏は、列車の床にそなえつけた光源から列車の天井の鏡めがけて垂直に光を発する。その結果、光は、天井の鏡で反射されて床に戻る。
【Y氏が行うこと】
列車の外から、列車の中のX氏が床から発した光が、鏡で反射されて床へ戻るのを見る。
簡単な状況である。X氏が列車の床から発した光が列車の天井と床を往復するのをY氏も見る、ということだ。
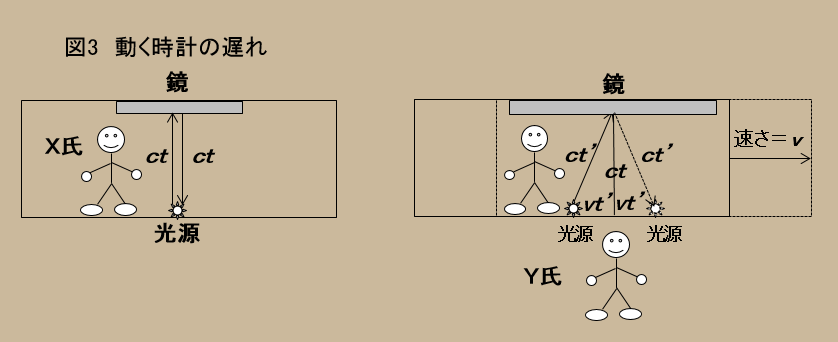
X氏にとっては、光が、行った道をそのまま返るだけである。その事実はY氏が見ても変わらない。ただY氏から見てX氏が動いているので、Y氏にとっては、光の道筋が単純往復に見えないだけである。
列車は、Y氏に対して速度($v$)で右へ走っているので、Y氏から見ると光は右上へ走り天井で反射してさらに右下に走る。このとき光が発せられて、天井に至るまでの時間を($t'$)とするとその間にX氏が動く距離は$(v)×(t')$である。そうですね。
ただ、気をつけなければいけないのは、X氏にとっても、Y氏にとっても光の速度は同じ$c$であるということだ。この時点では、あまりこのことを重要と思わないかもしれないが、以下を検討して行くと実に不思議な事が現れるのである。
さて、Y氏にとっては、光の走った経路に従って底辺($vt'$)、高さ($ct$)、斜辺($ct'$)の直角三角形が二つできる。さて、光が走った距離は? ピタゴラスの定理を持ち出すまでもなく、Y氏が見る距離のほうが、X氏がみる距離より長い。
光の速さがX氏とY氏で異なるならば、これは別に不思議なことではない。しかし、思い出して欲しい。光速度は常に、誰にとっても $c$ なのである(ダッシュはつかない)。
そうすると、ピタゴラスの定理より、 \[(ct')^2=(ct)^2+(vt')^2\] がいえる。Y氏が測る時間($t'$)をX氏の時間($t$)で表してみよう。 \begin{equation} (ct')^2 - (vt')^2 = (ct)^2 \\ t'^2(c^2 - v^2) = c^2t^2 \\ t'^2 = \frac{c^2t^2}{c^2 - v^2} \\ t'^2 = \frac{t^2}{1 - \frac{v^2}{c^2}} \\ t’ = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} \end{equation} つまり、Y氏が測る時間($t'$)はX氏の時間($t$)にローレンツ因子をかけたものになる。
そうでなければ、X氏とY氏にとって光速度 $c$ が同じにならないのだ。
\[\Large{\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}\tag{ローレンツ因子}\]
ローレンツ因子の分母は、1より小さくなるので因子全体では1よりも大きい値になる。
まとめ
ある慣性系から見て、動く物体の時間は、静止している側から見た時間にローレンツ因子をかけたものになる。(間延びする=遅れて見える)
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
5.思考実験その2(動く物体の収縮)
なんでこんな話をしているのか、わからないと思っている人は、大丈夫、正常である。
「アインシュタインの二つの原理まではわかったよ。でもなんで突然こんな話になるんだ?」と思わない方がおかしい。
そこで理屈を言う。アインシュタインの第1原理を思いだしていただきたい。
光速度は、いかなる慣性系から測定しても同じである(光速度不変の原理)これを認めると、相対速度を持って運動する物体同士の空間(長さ)と時間の関係が妙なものになってくるのだ。
なぜなら光速度は、誰がどのように観測しても一定なのに、それを観測する側が様々に動いているとすれば、速度が「距離/時間」である以上、そのしわ寄せは、「距離」と「時間」の双方で負わなければならない。つまり以下のように言える。
(1)私が見るあなたの時間は、あなた自身の時間と異なる。(前項にて説明ずみ)非常に不思議なことになって来ていることはおわかりだろう。自分に対してある速さで走っている者が持つ時計は遅れて観測される、つまり、あなたと私の時間は同じに進まない。「そんなばかな!」と叫びたくなる人は健全だ。
(2)私が見るあなたの長さは、あなた自身の長さと異なる。(本項にて説明する)
アインシュタインが、こんなことを言い出したから、相対論は、初めは誰にも相手にされなかったのだ。しかし光速度不変の原理を前提とするとそのようになってしまうのである。
さて、唐突に、本項の説明に入る。前項と同じ方式でやってみよう。
気をつけるのは、光速度は($c$)でX氏とY氏にとって同じ、その他の値はX氏とY氏で同じとは思いこまないようにすることだ。
【状況】
Yという人がいて、便宜上静止しているとみなす。(全ての慣性系は相対速度しか持たないので、今Y氏を基準の系とする。)このY氏の目の前を、(Y氏から見て)右へ速度($v$)で走っている列車がある。列車にはXという人(列車に対して静止)がいる。光速度は、お約束で($c$)で表す
【X氏が行うこと】
本項では、X氏は列車の中で後方から光を発し、列車の前方にある鏡で反射させ光源の位置へ戻すものとする。X氏にとっての列車の長さは($L$)である。
前項では光を垂直に往復させたのに対し、本項では水平に往復させるのである。
【Y氏が行うこと】
列車の外から列車の中のX氏が列車後方から発した光が列車方の鏡で反射されて列車後方へ戻るのを見る。
X氏にとっては、行きも帰りも光は同じ距離($L$)を走るのだから、時間($t$)は往復で同じであるが、Y氏にとっては、列車が動くので、光が鏡で反射する(行きの)時間を($t_1$)、列車後方へ戻る(帰りの)時間を($t_2$)と違う値で表しておく。Y氏とっては列車の長さも($L'$)とする。
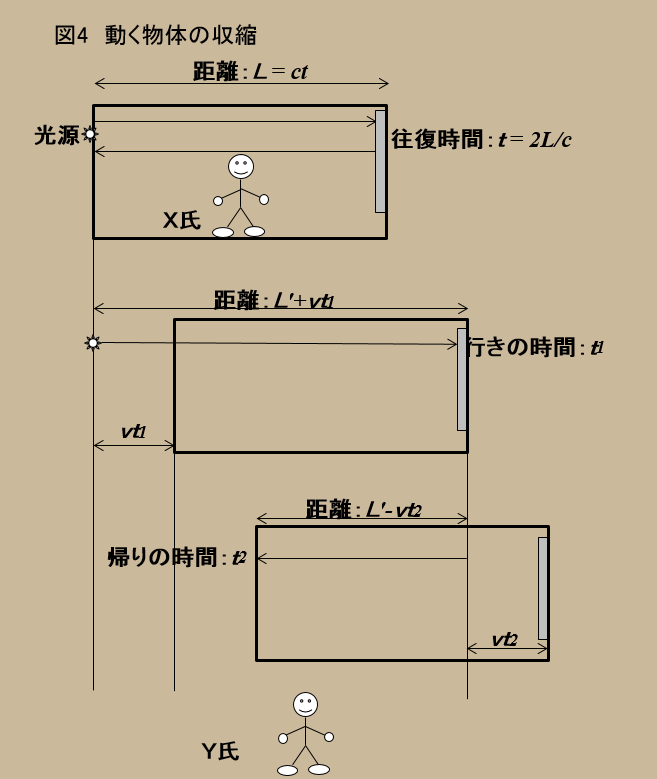
X氏にとって話は単純で、光が往復する距離は($2L$)、光速は($c$)なので、かかる時間は、 \[t = \frac{2L}{c}\] である。
対して、Y氏が測る距離は若干考慮を要する。(図4参照)
まず、行きでは、列車が速度(v)で右へ走っているので、光は$(L' + vt_1)$を走ったように見える。
対して帰りは、図のように、光は$(L' - vt_2)$走るだけで、列車の後部にたどり着く。
さて、整理してみよう。光速は誰にとっても($c$)なのだから、行きは \begin{equation} ct_1 = L' + vt_1 \\ ct_1 - vt_1 = L' \\ t_1 = \frac{L'}{c - v} \end{equation} と表せる。次に、帰りは、 \begin{equation} ct_2 = L' - vt_2 \\ ct_2 + vt_2 = L' \\ t_2 = \frac{L'}{c + v} \end{equation} である。よって、Y氏にとって光が往復する時間は、 \[t' = t_1 + t_2\] となるので、 \begin{eqnarray} t'&=& \frac{L'}{c - v} + \frac{L'}{c + v} \\ &=& \frac{L'(c + v) + L'(c - v)}{c^2 - v^2} \\ &=& \frac{2cL'}{c^2 - v^2} \end{eqnarray} ということが導かれる。ところが、前項の結論より、Y氏とX氏の時間の関係は \[t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}}\] なのであり、$t = \frac{2L}{c}$なのだから、 \begin{equation} \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{2cL'}{c^2 - v^2} \\ \frac{\frac{2L}{c}}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{2cL'}{c^2 - v^2} \\ L' = \frac{L(c^2 - v^2)}{c・c・\sqrt{1 - \frac{v^2}{c^2}}} = \frac{L(1 - \frac{v^2}{c^2})}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{L(1 - \frac{v^2}{c^2})\sqrt{1 - v^2/c^2}}{1 - \frac{v^2}{c^2}} = L\sqrt{1 - \frac{v^2}{c^2}} \end{equation} $\sqrt{1−\frac{v^2}{c^2}}$ は、ローレンツ因子の逆数であるから、Y氏が測る列車の長さ($L'$)はX氏が測る列車の長さ間($L$)をローレンツ因子で割ればいいことになる。
ローレンツ因子は1より大きくなるが、その逆数は1より小さくなる。
まとめ
ある慣性系から見て、動く物体の長さは、静止しているときの長さをローレンツ因子で割ったものになる。(縮む)
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
6.時空間での不変量
3項と4項でわかったことは、自分に対して相対速度を持った相手は、時計(時間)と長さ(空間)が自分の認識と相手の認識で異なってしまうのだ、ということだ。
皆さんには、これを素直に認めることをお勧めする。二つの原理がこの宇宙で実際に起こることなのだから、そこから理論的に導かれる事柄も正しいと認める勇気が必要だということだ。一部には己の信ずる常識と食い違うため、この事実を疑う方もいるかもしれない。特に、時間の進みが、私とあなたで異なるということに拒否反応を示す人は多い。
しかし、「物理学」が「人間が認識しうる自然現象を扱う学問」である以上、この結論を拒否することはできない。慣性系において光速がどんな立場のものにも一定に観測されるという事実が、「時間の遅れ」「長さの縮み」を引き起こすのである。そしてこれは必然なことなのである。
いかに信じられなくとも、次の事実を認めてほしい。
(1)私が見るあなたの長さは、あなた自身の長さと異なる。アインシュタインの発想のすばらしさは、長さ(空間)と時計(時間)を対等に扱おうとしたことである。
(2)私が見るあなたの時間は、あなた自身の時間と異なる。
(3)上記(1)と(2)は単独ではなく、共に起こる現実である。
とっても簡単な方法で、時間と空間を結び付ける式を示してみよう。
まず、三次元のピタゴラスの定理をおさらいしておこう。
点A$(x_1, y_1, z_1)$ と点Aと点Bの距離が$L$である(棒の長さが$L$である)とすると、 \[(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 = L^2\] である。つまり、空間のどこに棒をもっていっても、$L$という長さは不変量であることを言っている。みなさん、当たり前だと思ったでしょ。そう、常識では、これは当然のことである。
点B$(x_2, y_2, z_2)$ があり、これが空間内の棒の両端であるとする。
しかし第3項で示したように、光速度一定を前提にすると、相対速度を持った物体同士では、相手の長さが変わって観測されることを思い出してみよう。そうであれば、あなたと私の間に相対速度があれば、同じ棒の長さは変わって観測されることになる。
それでは、光速度が誰にとっても一定という条件の元で、いかなる慣性系においても不変となる量があるのだろうか。
それを考えてみることにしよう。
まず、二つの慣性系QとRを考える。
話を簡単にするために、時刻0においてQとRは、同じ場所にいた(つまり座標原点が一致していた)とする。そして、Rは、Qに対して相対速度($v$)で動いているものとする。
さて、ちょうどQとRの原点が一致していたとき。両慣性系は、各々同一の方向へ光を発した。
Qにとって($t_1$)の時間が経過したとき、Rでは($t_2$)の時間が経過したものとする。(相対速度を持つ慣性系では時間の進みは同じではない。)
Qにとっては、光は($ct_1$)の距離を進む。対して、Rでは、光は($ct_2$)の距離を進む。
さて各々の系での光の到達位置を考えると、時間を考慮した4次元の座標は
慣性系Q:点A$(x_1, y_1, z_1, t_1$)と表すことができる。
慣性系R:点B$(x_2, y_2, z_2, t_2$)
ここまではよいと思う。問題は次だ。
原点と点Aとの空間的距離の2乗は、 \begin{equation} (x_1 - 0)^2 + (y_1 - 0)^2 + (z_1 - 0)^2 \\ x_1^2 + y_1^2 + z_1^2 \end{equation} と書ける。
同様に原点と点Bとの空間的距離の2乗は、 \[x_2^2 + y_2^2 + z_2^2\] である。
ところが、点A点B共に、原点から光が走った距離と等しい。すなわち \begin{eqnarray} x_1^2 + y_1^2 + z_1^2 = (ct_1)^2 \tag{1}\\ x_2^2 + y_2^2 + z_2^2 = (ct_2)^2 \tag{2} \end{eqnarray} ということになる。
ここで(2)式から(1)式を引いてみよう。 \[(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 = (ct_2 - ct_1)^2\] これが、4次元時空間における点Aと点Bの距離を表す式である。
左辺は、ご存じ「空間距離」の2乗であるが、右辺は何だろう。単純な「時間距離」の2乗$(t_2 - t_1)^2$とはちょっと違っている。にしても、ある意味での「時間距離」の2乗と表現してももいいだろう。
つまり、4次元時空間では、時間を含めた事象の隔たりが不変量になるのである。よって3次元のピタゴラスの定理から、これを4次元時空間に応用して \[(x_2 - x_1)^2 + (y_2 - y_1)~2 + (z_2 - z_1)^2 - (ct_2 - ct_1)^2 = S^2\] と表すことができる。
これを整理すると
≪3次元空間のピタゴラスの定理≫ \[x^2 + y^2 + z^2 = L^2 \tag{$L$は、慣性系の座標原点からの距離}\] ≪4次元時空間のピタゴラスの定理≫ \[x^2 + y^2 + z^2 - (ct)^2 = S^2\] である。
時間の項にだけ光速度($c$)が掛かっており、さらに2乗の項がプラスでなくマイナスである。これは、えこひいきではないのか? と思う人は鋭い。しかし、不変定数($c$)を掛けることにより、時間を、空間と対等な単位にしたとき、2乗項がマイナスになるというのは、時間というものが虚数だと考えることもできる。人は空間を自由に移動できる(体感できる)のに対し、時間は、人の意思とは関係なく流れ行き見えない(体感できない)のは、このためではないのか、という考えもできる。
さて、($S$)とはなんであろうか。ここでは、4次元時空間における事件(時間も含めた)の間の隔たり、と捉えておこう。
なにはともあれ、位置(事件)の四元量が定義できた。
位置(事件)の四元量 $( x, y, z, ct )$である。そしてここに不変定数光速($c$)が出てきたのだ。
一言いいたい!

【わかっても相対論 第2章 はじめに光速度ありき】
目次へ 次へ進む 前へ戻る
第2章の ま・と・め
アインシュタインは考えた。
光速度を一定値にさせるところのものが、この宇宙なのではないか?で、それを元に二つの原理を提唱した。
(1)光速度は、いかなる慣性系から測定しても同じである(光速度不変の原理)どんな立場にいる人も、等速運動している限り、光速は同じ、ということ。
(2)いかなる慣性系でも、物理現象は同じである(特殊相対性原理)
従って、どんな人も、立場が違えば、長さ(空間)と時計(時間)の両方が、同一でなくなる、ということ。
空間 $(x, y, z)$ と、時間 $(t)$ をえこひいきなく仲間にして、を考えよう。
4元位置 $(x, y, z, ct)$
このとき、4次元時空間のピタゴラスの定理は、 \[x^2 + y^2 + z^2 - (ct)^2 = S^2\] である。
次章へ 一言いいたい!
