�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�P�D�����ɓ�����
���������A���̉F���ŕ����ɓ����͂̎�ނƂ��āA�����܂łɁA����m���Ă��邩���m�F���Ă��������B�i�O�͂܂ł̂����炢�ł���B�j
�܂��A�i�P�j���d���ł��邪�A����݂͂Ȃ���������Ȃ��Ƃ����ɂ������肾�낤�B�j���[�g�����������A������u���L�����v�̂��Ƃł���B�����Ǝ��ʂ̊Ԃɓ������͂̂��Ƃ��B�A���A�u�킩���Ă����Θ_�v�ł́A�d�͂ȂǂƂ����͂͑��݂����A����͊w�I�Ȏ���Ԃ̋Ȃ���Ƃ��Đ��������A�ƌ������B�����āA�u�Ȃɂ͂��Ă����ʎq�_�v�́A�ʎq�_�I�u���v�̊T�O�ł́A���z�d�͎q����ь����Ƃ���A�ƒ�`�����̂ł���B�i���̎���痝���ł��Ȃ��l�͌��S�ł���B�m�肽����A�u�킩���Ă����Θ_�v�Ɓu�Ȃɂ͂��Ă����ʎq�_�v�����Q�������K���Ă݂悤�B�j
���ɁA�i�Q�j���d���C���́A�u�d���v�y�сu���C�v�������������Ԃɓ����͂̂��Ƃ��B�ʎq�_�I�u��v�̊T�O�ł́A�u���z���q�v�̔�ь����Ƃ���A�ł���B
�����āA�i�R�j�́A�O�͂̍Ō�Ō��ꂽ�A�j�q�Ɗj�q�̊Ԃɓ������͂ł���B
�z�q�Ɨz�q�̊Ԃɓ����N�[�������i�˗́j�́A�d�ד��m�̋����̓��ɔ���Ⴕ�ď������Ȃ�B�t�Ɍ����A�������߂��قǑ傫���B���q�j�̑傫���i��$10^{-15}m$�j�̒��ɕ����̗z�q�����݂��邱�Ƃ��l����A���̗͂ɋt����Ċj�q�����т���̂�����A���̗͂͋ɂ߂đ傫���ƌ��_�ł���B
���̊j�q�Ԃɓ����͂��A���ꂩ��́u�j���v�ƌĂԁB
�Ƃ���ŁA�A�O�͂Ŏ��́A���̊j�͂ɂ͎O��ނ���̂ł͂Ȃ����H�@�Ƃ����^�������B
����G�����m��m���Ă��āA���̌��тœ��{�l�����m�[�x��������܂����̂����m���Ă���Ȃ�A�j�͂�}��闱�q��m���Ă���l���������Ƃ��낤�B������A���̎O��̗͂���ʂ���K�v����F�߂Ȃ��l���������邾�낤�B
�Ȃ�A�t�ɕ��������B$p$�i�z�q�j��$n$�i�����q�j���قȂ�f���q�ł���ƔF�����Ă��鍡�A��L�̎O��̗͂������ł���ƌ��_���闝�R�͂����������Ȃ̂��A���Ȃ��͐����ł��邩�H
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�Q�D�x�[�^����
���q�j�����ł̗́A����
�O���ōŌ�ɒ������Ƃւ̓������������B
�܂��ЂƂ��k�ق����������Ƃ���������B����́A
�u$p$�i�z�q�j��$n$�i�����q�j���قȂ��f���q�ł���ƔF�����Ă��鍡�A��L�̎O�킪�����ł���ƌ��_���闝�R�v�Ƃ������͂ł���B
�d���́A�u�����v�������q�Ԃɓ����͂ł���A�������q�Ԃ����ɓ������̂ł͂Ȃ��B���l���d���C�����A�u�d���v�����S�Ă̗��q�Ԃɓ������̂ł���A�������q�Ԃɓ������̂ł͂Ȃ��B
������A�u�j�́v�����āA�������q�Ԃɓ����K�v�͑S�R�Ȃ��B�]���ď�L�@�`�B�������͂ł��邱�ƂɁA���̖����Ȃ��B���ɂȂ�̂́A�u�j�́v���u�ȂɁv�����������q�Ԃɓ����͂Ȃ̂��H�@�Ƃ������Ƃł���B
�{���́A�����������Ɖ������Ȃ���A��L�@�`�B�͓������̂ł���Ƃ͌����Ȃ��̂��B
�Ƃ��낪�A���씎�m���j�͂�}��闱�q�Ƃ��āu���Ԏq�v�������o�����Ƃ��A���́A���́u�ȂɁv���A�������Ă��Ȃ������ɂ�������炸�A�S�R���ɂ���Ȃ������B�܂�A�z�q�ƒ����q��}���͂́u���ɂȂ���́v�͕s���̂܂܂������̂ł���B�i���씎�m����Ă����ł͂Ȃ��̂Ō���Ȃ��悤�B�j
���̂悤�ɁA�͂̌����s���Ȃ̂ɁA�u���Ԏq�v���o�ꂵ���̂ɂ́A���R������B
����́A�u�z�q�v�́u�����q�v�ɁA�u�����q�v�́u�z�q�v�ɕς�肤��A�Ƃ������������ɒm���Ă�������ł���B������A���q�j���ł���͋N����B���q�j���ł��̌��ۂ��N����ȏ�A�z�q�ƒ����q�́A�u�P�ꗱ�q�̈قȂ��ԁv�ƌ��Ȃ����Ƃ��ł��A��L�@�`�B����ʂ���K�v���Ȃ������̂ł���B���������Ċj�͈͂��ށB���ꂪ�������B
�⑫
�����q�́A���q�j�O�ł��z�q�ɕς�邱�Ƃ��ł��邪�A�z�q�͌��q�j�O�Œ����q�ɕς�邱�Ƃ��Ȃ��B�i�{���́A�����������Ă��܂��Ă͂܂����̂����A����ɂ��ẮA���[���ƌ�ŏq�ׂ�B������������A�y����ҁz�ł͂Ȃ���������Ȃ��B�j
���q�j���ŁA�u�z�q�v���u�����q�v�ɁA�u�����q�v���u�z�q�v�ɕς�錻�ۂ��u�x�[�^�����v�Ƃ����B
���U�t�H�[�h�����q���f���\�����P�X�P�P�N�̂Q�N��A�p�E�����A���Ɍ��ۂƂ��Ă͒m���Ă����x�[�^������������A���̂悤�Ȍ��_���o�����B
�����q�ߏ�̌��q�j�ł́A�j���̒����q���A�z�q���d�q�y�����j���[�g���m�ɕ���B
���ɁA�z�q�ߏ�̌��q�j�ł́A�j���̗z�q���A�����q���z�d�q�y�уj���[�g���m�ɕ���B
���ӂP
���R�E�ɑ��݂��錴�q�j�́A�����q���z�q�Ɠ��������A�܂��͑����B���������Č��ۓI�ɂ́A$\beta^{-}$����̕���$\beta^{+}$�����舳�|�I�ɑ����B�܂��A�⑫�ŏ������悤�ɁA���̒����q�͎��R��$\beta^{-}$������N�������߁A�x�[�^����Ƃ����ƁA$\beta^{-}$����̂��Ƃ��Ǝv���Ă��邢��l�������B���̋@���$\beta^{+}$������o���Ă����Ƃ悢�B
���ӂQ
���̍��ł́A�z�d�q�E�j���[�g���m�y�є��j���[�g���m�A�X�ɒ��Ԏq�܂ł����o�ꂵ�����A���̍��ł́A�Ƃ肠�����A����Ȃ��̂�����A�Ƃ����F�����Ă��炢�����B�ڍׂ͕ʓr��������B
���āA�O��ނ̊j�͓͂���ł��邱�Ƃ����������B�Ƃ���A�u$p-p$�ԗ́v�����A�d���C�́i�˗́j����������̂ŁA�j�q�̌��т����s����ɂȂ�B�����A���q�j�̐����i���f�j���A$p$�̐��Ō��܂�Ȃ�A$p$�����łȂ��A$n$���������������q�j�͈���ɂȂ�̂ł���B�i$p$��$p$�̊Ԃɓ����āA$p$��$p$�̊Ԃɋ���������ڂƎv���悢�B�j�]���āA���q�j�ɂ͒����q�����݂��Ă悢�̂ł���B
�ŏ��́A�x�[�^������N�����͂��j�͂ł���A�ƍl����ꂽ�������������B�܂茴�q�j���ŁA$p$��$n$�ɁA$n$��$p$�ɕϊ����邱�Ƃɂ��A�����Ɉ��͂����܂��A�Ƃ����_�@���B��������闱�q�́A�d�q�i�z�d�q�j�Ɣ��j���[�g���m�i�j���[�g���m�j�ł���B�������A�^����������B����́A�������Ă��闱�q���A�o���ňقȂ邱�Ƃ��B
����ɁA���̃x�[�^����ɂ�茻���͂��v�Z���Ă݂�ƁA�d���C�͂�肸���Ə��������Ƃ����������̂��B���̗͂ł͊j�q���܂Ƃ߂邱�Ƃ͑S���s�\�������̂ł���B
���Ƃ���A���̃x�[�^����Ƃ������ۂ́A�����������Ȃ̂��Ƃ����^�₪�N���B�������A�����̗͂ł��邱�Ƃ͊m���ł���A���̗͂��u�ア�́i���ݍ�p�j�v�Ɩ��t�����邱�ƂɂȂ����B
�i���q�Ԃɓ����́A�Ƃ�������j�q�̕���𑣂����Ƃ��Č����̂ŁA�ア���ݍ�p�Ƃ��Ă��̂ł���B�j
����ŁA�������͎��R�E�̂S�̗͂�m�����B
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�R�D���Ԏq
���āA�O���܂łɏo�Ă����f���q�����Ă������B
�d���C�́i�N�[�������j�́A���q���L���b�`�{�[���ɂ�蔭������B
�d�͂́A�������̗��q�ł����d�͎q�i�O���r�g���j�̃L���b�`�{�[���ɂ�蔭������i�ƍl�����Ă���j�B
�ア���i�x�[�^�����j�́A���ʉ����}��i�H�j���Ă��邩�s���ł���B
����ł́A�j�͂�}��闱�q�͉����H
�{�����t���C���O�Ȃ̂����A�O���Ŗ��O���������Ă��܂����B
����G�����m�́A���̗��q���������v�Z�ŋ��߁A�d�q���j�q�̒��Ԃ��炢�i�d�q��$200$�{���j�ł���Ɨ\�����A����Ɂu���Ԏq�v�Ƃ�������t�����B����āA�j�͂Ƃ́A���Ԏq��ł���A�Ƃ������ƂɂȂ����B
�]�k
���́A����́u���Ԏq�_�v�͔��ɕ]�������������B���R�́A���m�̗��q�����肷��A�ǂ�Ȏ��R���ۂł������ł��Ă��܂��A�Ƃ������Ƃ���ł���B�X�ɁA���Ԏq�����̌��ɂȂ�u�Ȃɂ��v�������ł��Ă��Ȃ����Ƃ����R�̂ЂƂ�������������Ȃ��B
�ʎq�_��Ă̐e�ŗL�����{�[�A�����������Ƃ��A�M�S�ɒ��Ԏq�_���������ɑ��A�u�N�́A����ȂɐV�������q���D�����B�v�Ɨ��₩�Ɍ������A�Ƃ����b�͗L�����B
�܂��A�i�{�����ǂ������m�F�̉\�ł��邪�j����Ɠ����悤�ɒ��Ԏq�_���v�������V���e�B�P���x���N�Ƃ����w���́A�搶�ł����p�E���ɁA�u��������܂���������Ƃ����āA����ȗ��q�����肷�����Ȃ��B�v�ƁA�_�����p������Ă��܂����Ƃ����b������B
�b�x��
�Ƃɂ����A���]�Ȑ܂͂��������̂́A����F�����̊ϑ��ɂ��A���́u���Ԏq�v�͔�������A���ʂ��d�q��$260$�{���x�ł��邱�Ƃ��m�F����A�j�͂�}��闱�q�Ƃ��ĔF�߂�ꂽ�B�i���Ԏq�_�́A�P�X�R�T�N�ɔ��\����A���Ԏq�̊m�F�͂P�X�S�V�N�������B�j
�t�������Ă����ƁA���Ԏq���j�͂�}���͈͂͋ɂ߂ď������i���ꂪ�A�������q�j�̑傫���ɂȂ�j�A���̗͂̑傫���͓d���C�͂�$100$�{�ł���B���̂��߁A���q�j�͋ɂ߂ď����ȗ̈�ɂ������݂ł��Ȃ��B
�����ŁA�{���́A�I�グ�ɂ��Ă������A�u�j�͂������錳�ɂȂ�ʁv�̘b�����Ȃ���Ȃ�Ȃ��̂ł��邪�A���闝�R�ɂ���A���̐����͍��̒i�K�ł͂ł��Ȃ��B���̘b�́u�펯�ҁv�łȂ��Ƃł��Ȃ����R������B�i�m���Ă���l�́A�b�������āA�����������Ă��邩������Ȃ����A�l�^�o���͍T����B���̂ɂ͏����Ƃ������̂�����B�j
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�S�D�ア��
�O���ł́u�ア���i�x�[�^�����������N�����́j�́A���ʉ����}��i�H�j���Ă��邩�s���ł���v�Ə������B
�d���ɑ��ẮA�i�������ł͂��邪�j�d�͎q�i�O���r�g���j������B
�d���C����}���̂́A���q�i�t�H�g���j�ł���B
�����āA�j����}���̂��A�O���Ő����������Ԏq�Ȃ̂ł������B
����ł́A�u�ア���v�͉����}���̂��H�@���������A�ア�͂́A���������������ē����͂ȂH�@�Ƃ����^��͓��R�ł���B
���́A�u�ア�́v�́A�j�q���u�E�B�[�N�{�\���v�Ƃ������q�Ƒ��ݍ�p����̂ł���B
����������ƁA�E�B�[�N�{�\�����ɂ����āA���z�E�B�[�N�{�\�����A�j�q�����ݍ�p����ƁA�j�q�̕ϊ��i�����q���z�q�ɁA�z�q�𒆐��q�Ɂj���N�����A���z�E�B�[�N�{�\�������̉����A�ɒZ���Ԃ��d�q���j���[�g���m�ɕ���̂ł���B�i���ǂݕԂ��Ȃ��ƁA������Ȃ��Ǝv���B�j
���܂łɓo�ꂵ�āA�����ł��Ă����d�������A�E�B�[�N�{�\����ɒu�������čl���Ă݂�B
�j�q�́A���z�E�B�[�N�{�\�����o������A�z�����肵�Ă���B�i������ċz����A�ƕ\������B�j
�����ċz���Ă��邾���Ȃ牽���N����Ȃ����A���܂��܂͂��o�������z�E�B�[�N�{�\����ʂ̗��q���߂܂��Ă��܂��ƁA���̗��q�Ԃɗ͂������B���ꂪ�u�ア�́v�ł���B�@�����܂ł͂悢�B�������A���̐悪���܂������ł��Ȃ��Ȃ�B
�Ⴆ�A�d����ł́A
������ア�͂ɂ��Ă͂߂Ă݂��
�N�����Ă���̂̓x�[�^���B�u�ア�́v�ƃx�[�^������Ȃ������͉��Ȃ̂��A�����l�������Ȃ��́A�Ƃ��Ă��܂Ƃ��ł���B�@�����ŁA���ꂩ�炻����������B
�N���肤�錻�ۂ̎�ނ́A
�@�i�P�j�z�q���͂��o�������z�E�B�[�N�{�\����z�q���߂܂����ꍇ
�@�i�Q�j�z�q���͂��o�������z�E�B�[�N�{�\���𒆐��q���߂܂����ꍇ
�@�i�R�j�����q���͂��o�������z�E�B�[�N�{�\���𒆐��q���߂܂����ꍇ
�@�i�S�j�����q���͂��o�������z�E�B�[�N�{�\����z�q���߂܂����ꍇ
�ȏ�A�S�ʂ肪�l������B�i�٘_�͂���܂���ˁB�j
�����S���Ђ�����߂Đ������邽�߂ɂ́A���z�E�B�[�N�{�\���Ƃ́A�j�q�ԂɁA���́E�˗͂������炷�̂ł͂Ȃ��āA�z�����j�q��ϐg�������ƍl���Ȃ���Ȃ�Ȃ��B
���A���z�E�B�[�N�{�\�������Ɂi$W$�j�ŕ\������ƁA��L�i�P�j�̃P�[�X�ł́A
��Q���F�Е��̗z�q�����z�E�B�[�N�{�\������o����
��R���F��������̗z�q�����z�E�B�[�N�{�\����߂܂���
��S���F���̌��ʁA�z�q�̓x�[�^����i��+�j���N�����A�����q�ɕς����
�S���̍�����A���́i$p$�j������Ă��܂��A
���l�Ɂi�Q�j�`�i�S�j���l���Ă݂�B
�i�Q�j
�@$\beta^{+}$����
�����āA���̃E�B�[�N�{�\���������錳�ɂȂ�ʂ��u��ׁi�E�B�[�N�ׁj�v�Ƃ����B�Ȃ���Ⴀ�A�Ǝv���l�͐���ŁA�����g���̖��O�̕t�����͂��܂�ɂ������ł���A�Ƃ�����Ă���B
����������Ă���̂́A�u�j�q�v�Ɓu�d�q�v�Ɓu�j���[�g���m�v�i�x�[�^���̂܂�܂ł���j�Ƃ������ƂɂȂ�A�E�B�[�N�{�\����ł́A�j�q���x�[�^����̂ł���B
�����l���Ă���ƁA����Ȃ��ƂɋC�Â��B����́A�Ⴆ�A��������̊j�q�������ł͂��o�������z�E�B�[�N�{�\���������Ōċz���Ă��x�[�^�����Ȃ����A�Ƃ������Ƃł���B
�����A���̋^������Ă���A�����A���̋^�₾���ŁA�����f���q�_�̒P�ʂ����炦��B
���ۂɂ���͋N���Ă���B�O�ɏ������͂����B�u���̒����q�́A�����Ă����ƁA$\beta^{-}$���āA�z�q�ɕς��v�ƁB
����́A�܂��Ɏ������g�����o�����E�B�[�N�{�\���Łu�ア���ݍ�p�v�����Ă���̂ł���B
���Ⴀ�A�Ȃ�ŗ��̗z�q�́A�����q�ɂȂ炢�H�@�Ƃ����^�₪�ł��s���w�E�Ȃ̂��B����́A�ƂĂ��Ȃ��䂾�����̂ł���B�C����������悤�ň������A���̉́A�w�킩��܂őf���q�_�u�펯�ҁv�x�ŏ������Ƃɂ���B�i�[�����R������̂ŁA�����Ă��������B�j
����ŁA�S�̗͂����̎p�m�Ɍ������B
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�T�D�t�@�C���}���E�_�C�A�O����
�O���ł́A�ア�����������q�Ƃ��̎d�g�݂͂Ǝ������Ő��������̂ŁA�ǎҏ����ɂ͍��������������̂Ɛ��@����B
���ۂɕ����w�ҒB���A�f���q�_�i��̗ʎq�_�ƌ��������Ă������j�ɂ����ẮA�N�����Ă��邱�Ƃ��I�ɗ�������̂ɋ�J�������j������̂ł���B
�č��ɁA���`���[�h�E�t�B���b�v�X�E�t�@�C���}���Ƃ��������w�҂������B�P�X�W�W�N�ɖS���Ȃ��Ă���̂����A���̑�w����̋��ȏ��́u�t�@�C���}�������w�v�������B���̋��ȏ��̂����b�ɂȂ����l�͑����̂ł͂Ȃ����Ǝv���B�ނ́A�P�X�U�T�N�ɓ��{�����i�U��Y���A�č����W�����A���ES�E�V���C���K�[���ƂƂ��ɁA�ʎq�d���C�w�̕�����m�[�x�������w������܂���ȂǗl�X�Ȍ��т�����̂����A�ł��L���Ȃ̂��A�{���Ŏ��グ��u�t�@�C���}���}�i�_�C�A�O�����j�v�ł���B
�t�@�C���}���}�Ƃ͉����������Ő������邱�Ƃ́A�t�@�C���}�����Ɏ���ł���B�Ȃɂ��땨���w�����o�I�ɕ\������\�͂ł͉E�ɏo����̂����Ȃ��ƌ���ꂽ���Ȃ̂�����A�����͐��������ŁA�t�@�C���}���}�����Ă��炨���B
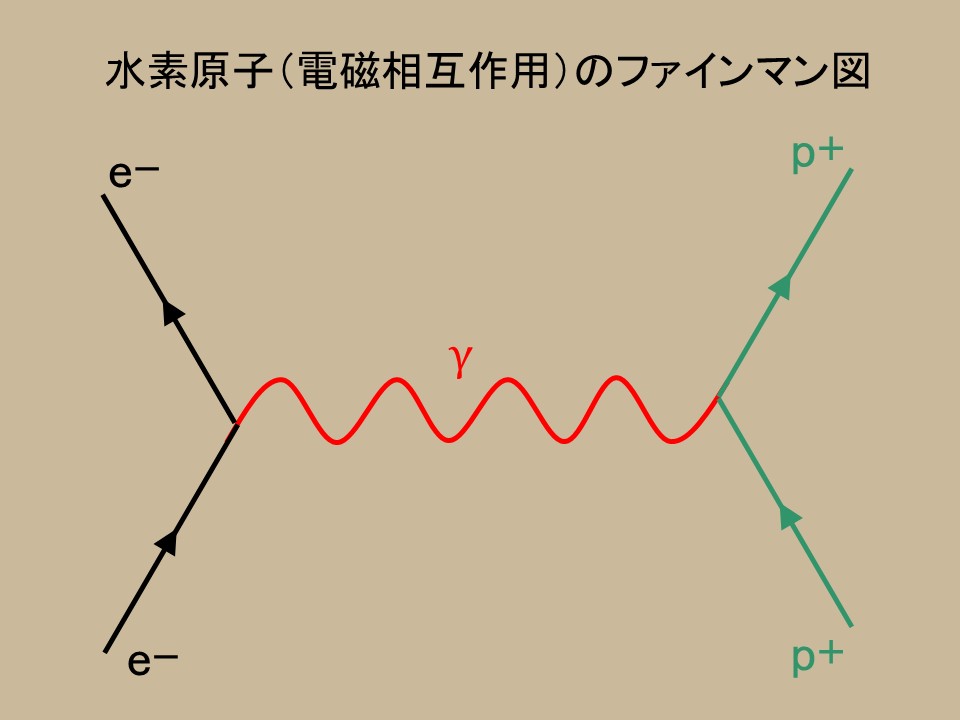
��}�́A���f���q�i�z�q���d�q�j�ɂ������d���C�́i�d�����ݍ�p�j��\�����t�@�C���}���}�ł���B���������[���������āA����𗝉�����Η��q�����ݍ�p����ڗđR�Ɍ��Ď�邱�Ƃ��ł���D����̂ł���B
�����́A�������q�i�z�q�A�����q�A�d�q�Ȃǁj��\���B�g���͗͂�}��闱�q�i���q�A�E�B�[�N�{�\���Ȃǁj�������B�����ɂ͖���Ă���̂ŁA�ω������邱�Ƃ��ł���B
�T�ˁA���̂��炢�𗝉�����A�������Ă킩��͂��ł���B
�E���ɗz�q�i$p$�j�������āA�����ɂ͓d�q�i$e^{-}$�j������B�z�q���d�q���ω����Ȃ��̂����A�g���̌��q�i$\gamma$�j���o�Ă���Ƃ���Ő܂�Ȃ����Ă��Ē��_���ł��Ă���B�����ŗ͂��`����Ă���ƌ���悢�̂ł���B
�z�q�i$p^{+}$�j�Ɠd�q�i$e^{-}$�j�̊Ԃ����q�i$\gamma$�j���s�������āA�N�[�����͂��������Ă��邱�Ƃ������Ă���B
�P�ɗ͂��`��邾���Ȃ�A�d�����A�j���������_�C�A�O�����Ŏ������Ƃ��ł���̂����A���́u�ア�́i���ݍ�p�j�v�ł���B
���̐}�����Ă��炢�����B
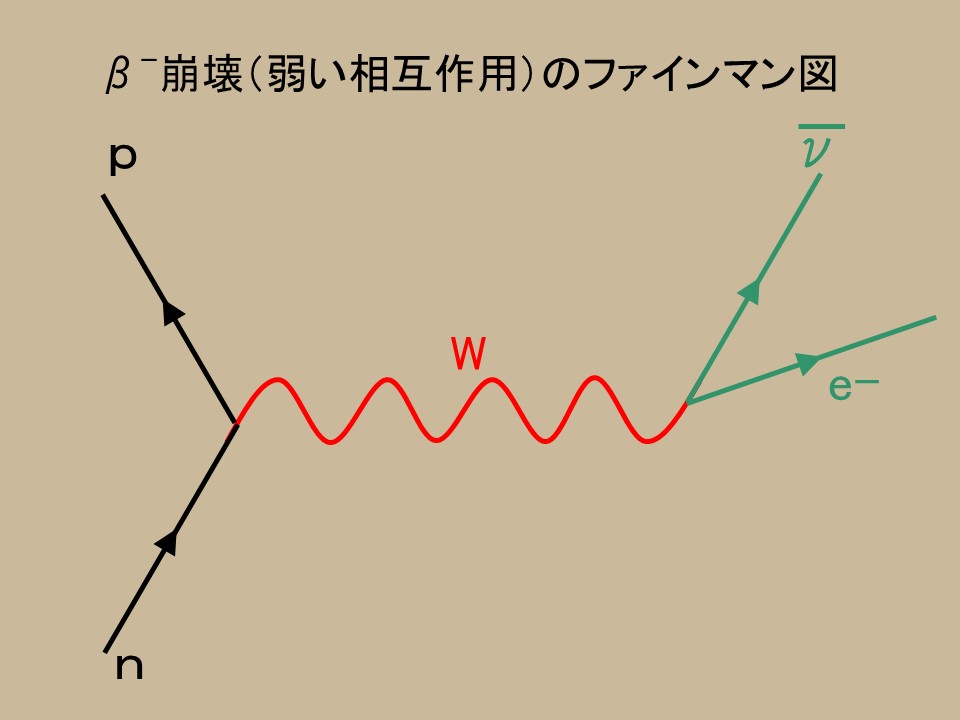
�����ɂ͒����q�i$n$�j������A�E�B�[�N�{�\���i$W$�j����āA�����q�i$n$�j���z�q�i$p$�j�ɕω����Ă���B�����āA�E�B�[�N�{�\���i$W$�j�͕��o��ŁA�d�q�i$e^{-}$�j�Ɣ��j���[�g���m�i$\overline{\nu}$�j�ɕ��Ă���B
���ꂪ�܂���$\beta^{-}$�����Ȃ̂ł���B
���̂��Ƃ��A�@�����t�@�C���}���}��p���āA��������Ղ����čs������ł���B
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�U�D���Ԏq�̎���
�j�������Ԏq���`����Ƃ������ƂŘb�����Ă����B���������O���ŏo�Ă����t�@�C���}���}���g���Ċj�͂��݂Ă݂悤�B�����Œ��Ԏq��$\pi$�ŕ\�����Ƃɂ���B
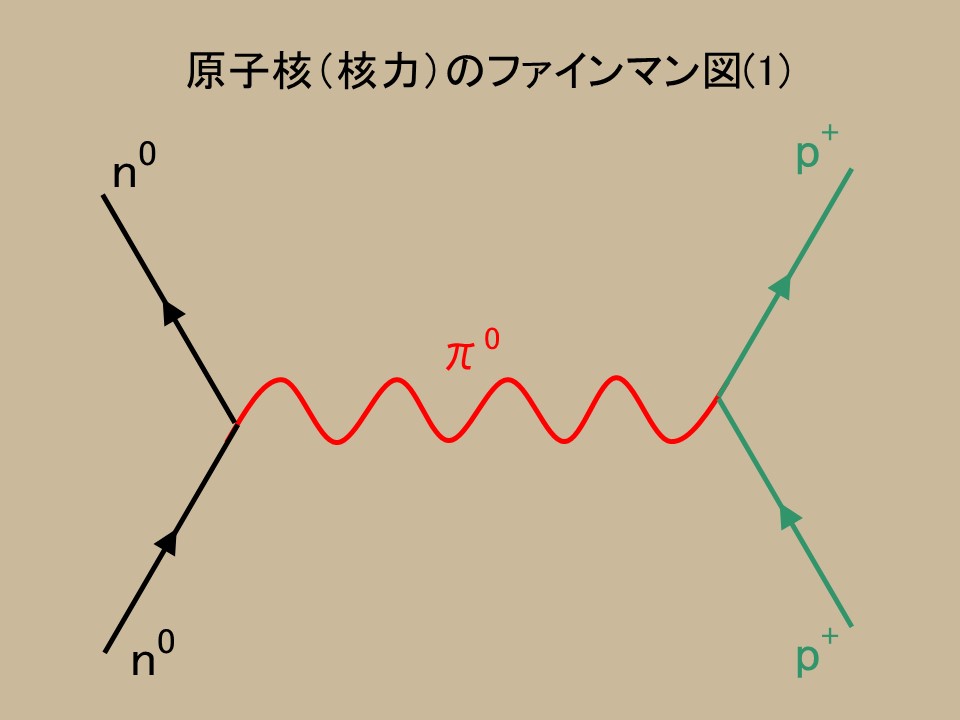
��}�́A�����q�i$n$�j���z�q�i$p$�j�����т��ۂ̃t�@�C���}���}�ł��邪�A�z�q�|�z�q�A�����q�|�����q�ł����Ă��͓����ł���B���Ԏq���L���b�`�{�[�����Ă��A�z�q�A�����q�͕ω����Ȃ��B���������āA���Ԏq���d���[���ł���B
�������A���Ԏq�ɓd�ׂ����������̂�����Ƃ���ƁA�ȉ��̂悤�ȑ��ݍ�p���l���邱�Ƃ��ł���B
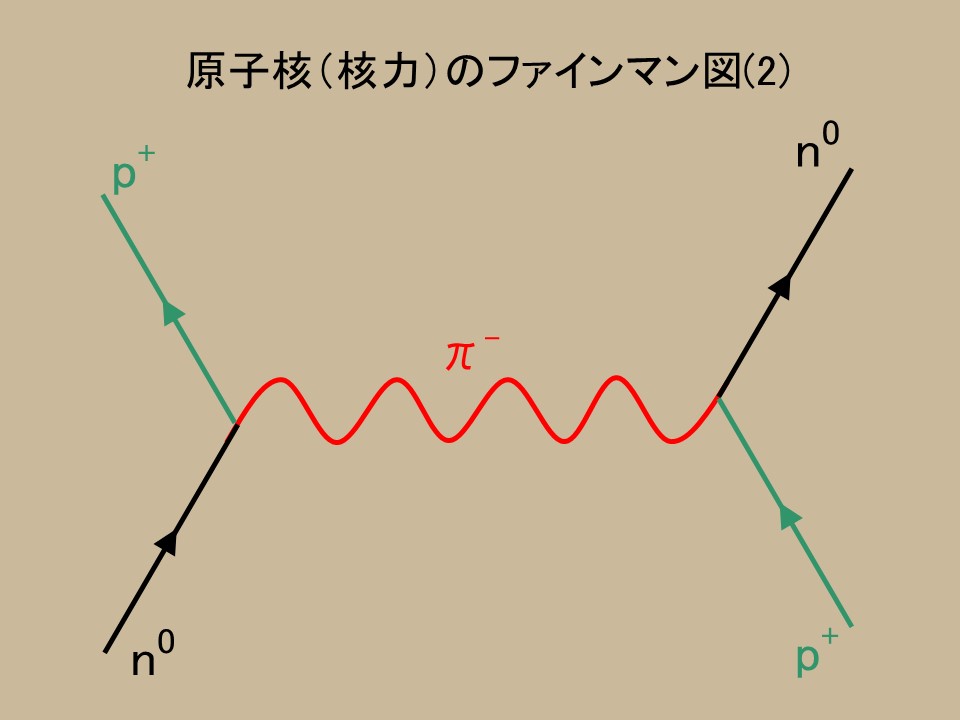
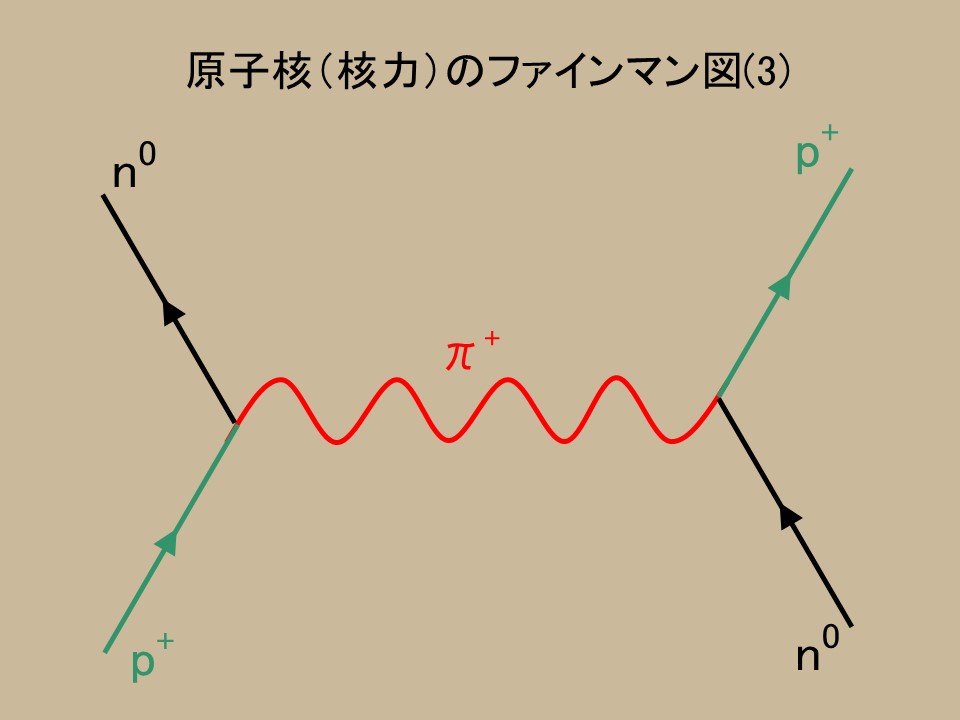
�d�ׂ����������Ԏq���L���b�`�{�[������ƁA�z�q�������q�ɁA�����q���z�q�ɕς��̂ł���B�����A�ǂ̏ꍇ�ł����q�j���̗z�q�A�����q�̐����ω����Ȃ��̂ŎO�̂����̂ǂꂪ�N�����Ă���̂�����ʂ���Ӗ����Ȃ��B
�x�[�^�����i�ア���ݍ�p�j�̗��_�́A�t�F���~�ɂ���č��ꂽ���A�����͂܂��ア�͂�}��闱�q�Ƃ������z���Ȃ������̂ŁA�P���ɒ����q���z�q�Ɠd�q�����j���[�g���m�ɕ�����̂��ƍl�����Ă����i�E�B�[�N�{�\�����o�ꂷ��̂́A��̗ʎq�_�����W���Ă䂭�P�X�V�O�N��ł���j�B
�����͒��Ԏq�_�\�����Ƃ��ɁA�x�[�^����ɑ��āA���̂悤�ȉ��߂������Ă����悤�ł���B
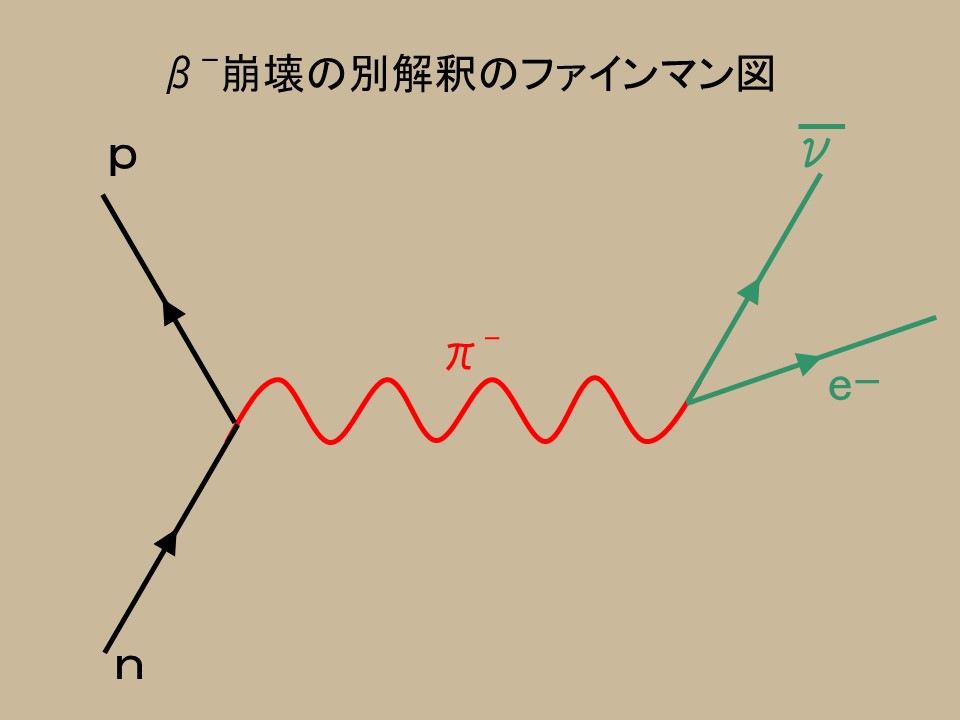
�܂�A���o�������Ԏq��߂܂��鑊�肪���Ȃ��ƁA���Ԏq���d�q�Ɣ��j���[�g���m�ɕ��ăx�[�^���N����Ƃ����}�����B
���̃A�C�f�A�͎��ۂɂ͂��܂��䂩�Ȃ��������A��̏�̗ʎq�_�ɂȂ�����тƂ��ĕ]������Ă���B
��������{���̖{��ɓ���B
�����������삪�j�͂�}��闱�q�ɒ��Ԏq�Ƃ������O��^�����̂́A���̗��q���A�j�q�Ɠd�q�̒��Ԃ��炢�����������ƌ��_�t�������炾�B�{���ł́A���̗��R��������Ɛ������Ă������B
�j�͂��d���C���̑傫�ȈႢ�́A�͂������������S���قȂ�_���B���������錴�q�j���̊j�q�������ȊO�̕ʂ����q�̌��q�j�ɓ����قǂ̗͂ł�������A���q���m���j�͂ł������Ă��܂��A�����������̂悤�Ȏ��R�E�͑��݂��Ȃ��Ȃ��Ă��܂��B�]���āA�j�͂Ƃ́A���q�j�̑傫�����x�̗̈�ł��������Ȃ��悤�ȗ��Ȃ̂ł���B�i���͈̔͂Ƃ́A$10^{-15}m$�Ƃ����l�ł���B�j
����ɑ��āA�d���C�͂͌��Ⴂ�ɍL���͈͂ɓ����B���q�j�Ƃ��̎���̓d�q���֓��̒n�}�ŕ\�����}���v���o���Ăق����B�j�͂������͈͂������w�ɂ����ꂽ$1m$�̃{�[���ł���Ƃ�����A���̌��q�j�Ɠd�q�̊Ԃɓ����d���C�͂́A�֓���~�ɍL����قǑ傫���i���ۂɂ͓d���C�͂́A�����ɔ���Ⴕ�Ďキ�͂Ȃ邪�A�����I�ɂ͖����̉����܂œ`���͂Ȃ̂ł���j�B
����́A�͂�}��闱�q�̎��ʂɊW����B
���ɏq�ׂ��悤�ɁA�j�͂�}��钆�Ԏq�́A���q�j�͈̔͂ɂ������邱�Ƃ��ł��Ȃ��B����́A���Ԏq�����݂��Ă����鎞�Ԃ��ɒ[�ɒZ�����Ƃ��Ӗ����Ă���B
���������A�j�q�i�z�q�A�����q�j�����Ԏq����o����̂́A�G�l���M�[�ۑ����Ɉᔽ�����B���ʂ̓G�l���M�[�Ɠ����i$E=mc^{2}$�j�Ȃ̂�����A���Ԏq�̕��o�́A������G�l���M�[�ݏo�����ƂɂȂ�B
�Ƃ��낪�A������G�l���M�[�����܂�Ă��悢�Ƃ����P�[�X���������͂��ł���B���ꂪ�A�u���ԁv�Ɓu�G�l���M�[�v���s�m�萫�����ł���B�i�ڍׂ́A�u�Ȃɂ͂��Ă����ʎq�_�v�Q�Ɓj
$\Delta{t}$�̍ŏ��l�͌��߂邱�Ƃ��ł���B�܂�A���Ԏq�����̐��̍ō����x�ł�������i$c$�j�ŁA���q�j���i$s=10^{-15}m$�j��[����[�܂ő��鎞�Ԃł���B
����ŁA
���Ԏq���j�q�Ɗj�q�̑��ݍ�p��S���i�j�͂�}���j���߂ɂ́A�Œ�ł����ꂾ���̎��ʂ��ǂ����Ă��K�v�ɂȂ�̂ł���B
���͂��@�@�ꌾ���������I

�ڎ����@�@���i���@�@�O�֖߂�
�P�D�����ɓ�����
���������A���̉F���ŕ����ɓ����͂̎�ނƂ��āA�����܂łɁA����m���Ă��邩���m�F���Ă��������B�i�O�͂܂ł̂����炢�ł���B�j
�i�P�j�d���ȏ�̎O��ł���i�͂����j�B
�i�Q�j�d���C��
�i�R�j�j�q�Ԃɓ����́i����͂܂���̗́j
�܂��A�i�P�j���d���ł��邪�A����݂͂Ȃ���������Ȃ��Ƃ����ɂ������肾�낤�B�j���[�g�����������A������u���L�����v�̂��Ƃł���B�����Ǝ��ʂ̊Ԃɓ������͂̂��Ƃ��B�A���A�u�킩���Ă����Θ_�v�ł́A�d�͂ȂǂƂ����͂͑��݂����A����͊w�I�Ȏ���Ԃ̋Ȃ���Ƃ��Đ��������A�ƌ������B�����āA�u�Ȃɂ͂��Ă����ʎq�_�v�́A�ʎq�_�I�u���v�̊T�O�ł́A���z�d�͎q����ь����Ƃ���A�ƒ�`�����̂ł���B�i���̎���痝���ł��Ȃ��l�͌��S�ł���B�m�肽����A�u�킩���Ă����Θ_�v�Ɓu�Ȃɂ͂��Ă����ʎq�_�v�����Q�������K���Ă݂悤�B�j
���ɁA�i�Q�j���d���C���́A�u�d���v�y�сu���C�v�������������Ԃɓ����͂̂��Ƃ��B�ʎq�_�I�u��v�̊T�O�ł́A�u���z���q�v�̔�ь����Ƃ���A�ł���B
�����āA�i�R�j�́A�O�͂̍Ō�Ō��ꂽ�A�j�q�Ɗj�q�̊Ԃɓ������͂ł���B
�z�q�Ɨz�q�̊Ԃɓ����N�[�������i�˗́j�́A�d�ד��m�̋����̓��ɔ���Ⴕ�ď������Ȃ�B�t�Ɍ����A�������߂��قǑ傫���B���q�j�̑傫���i��$10^{-15}m$�j�̒��ɕ����̗z�q�����݂��邱�Ƃ��l����A���̗͂ɋt����Ċj�q�����т���̂�����A���̗͂͋ɂ߂đ傫���ƌ��_�ł���B
���̊j�q�Ԃɓ����͂��A���ꂩ��́u�j���v�ƌĂԁB
�Ƃ���ŁA�A�O�͂Ŏ��́A���̊j�͂ɂ͎O��ނ���̂ł͂Ȃ����H�@�Ƃ����^�������B
�@$p-p$�ԗ́i�z�q�Ɨz�q�ɓ����́j�̎O��ނł���B
�A$n-n$�ԗ́i�����q�ƒ����q�ɓ�����
�B$p-n$�ԗ́i�z�q�ƒ����q�ɓ����́j
����G�����m��m���Ă��āA���̌��тœ��{�l�����m�[�x��������܂����̂����m���Ă���Ȃ�A�j�͂�}��闱�q��m���Ă���l���������Ƃ��낤�B������A���̎O��̗͂���ʂ���K�v����F�߂Ȃ��l���������邾�낤�B
�Ȃ�A�t�ɕ��������B$p$�i�z�q�j��$n$�i�����q�j���قȂ�f���q�ł���ƔF�����Ă��鍡�A��L�̎O��̗͂������ł���ƌ��_���闝�R�͂����������Ȃ̂��A���Ȃ��͐����ł��邩�H
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�Q�D�x�[�^����
���q�j�����ł̗́A����
�@$p-p$�ԗ��̎O��ނ̈��́i�j���j���Ȃ��������̂Ȃ̂��H
�A$n-n$�ԗ�
�B$p-n$�ԗ�
�O���ōŌ�ɒ������Ƃւ̓������������B
�܂��ЂƂ��k�ق����������Ƃ���������B����́A
�u$p$�i�z�q�j��$n$�i�����q�j���قȂ��f���q�ł���ƔF�����Ă��鍡�A��L�̎O�킪�����ł���ƌ��_���闝�R�v�Ƃ������͂ł���B
�d���́A�u�����v�������q�Ԃɓ����͂ł���A�������q�Ԃ����ɓ������̂ł͂Ȃ��B���l���d���C�����A�u�d���v�����S�Ă̗��q�Ԃɓ������̂ł���A�������q�Ԃɓ������̂ł͂Ȃ��B
������A�u�j�́v�����āA�������q�Ԃɓ����K�v�͑S�R�Ȃ��B�]���ď�L�@�`�B�������͂ł��邱�ƂɁA���̖����Ȃ��B���ɂȂ�̂́A�u�j�́v���u�ȂɁv�����������q�Ԃɓ����͂Ȃ̂��H�@�Ƃ������Ƃł���B
�{���́A�����������Ɖ������Ȃ���A��L�@�`�B�͓������̂ł���Ƃ͌����Ȃ��̂��B
�Ƃ��낪�A���씎�m���j�͂�}��闱�q�Ƃ��āu���Ԏq�v�������o�����Ƃ��A���́A���́u�ȂɁv���A�������Ă��Ȃ������ɂ�������炸�A�S�R���ɂ���Ȃ������B�܂�A�z�q�ƒ����q��}���͂́u���ɂȂ���́v�͕s���̂܂܂������̂ł���B�i���씎�m����Ă����ł͂Ȃ��̂Ō���Ȃ��悤�B�j
���̂悤�ɁA�͂̌����s���Ȃ̂ɁA�u���Ԏq�v���o�ꂵ���̂ɂ́A���R������B
����́A�u�z�q�v�́u�����q�v�ɁA�u�����q�v�́u�z�q�v�ɕς�肤��A�Ƃ������������ɒm���Ă�������ł���B������A���q�j���ł���͋N����B���q�j���ł��̌��ۂ��N����ȏ�A�z�q�ƒ����q�́A�u�P�ꗱ�q�̈قȂ��ԁv�ƌ��Ȃ����Ƃ��ł��A��L�@�`�B����ʂ���K�v���Ȃ������̂ł���B���������Ċj�͈͂��ށB���ꂪ�������B
�⑫
�����q�́A���q�j�O�ł��z�q�ɕς�邱�Ƃ��ł��邪�A�z�q�͌��q�j�O�Œ����q�ɕς�邱�Ƃ��Ȃ��B�i�{���́A�����������Ă��܂��Ă͂܂����̂����A����ɂ��ẮA���[���ƌ�ŏq�ׂ�B������������A�y����ҁz�ł͂Ȃ���������Ȃ��B�j
���q�j���ŁA�u�z�q�v���u�����q�v�ɁA�u�����q�v���u�z�q�v�ɕς�錻�ۂ��u�x�[�^�����v�Ƃ����B
���U�t�H�[�h�����q���f���\�����P�X�P�P�N�̂Q�N��A�p�E�����A���Ɍ��ۂƂ��Ă͒m���Ă����x�[�^������������A���̂悤�Ȍ��_���o�����B
�����q�ߏ�̌��q�j�ł́A�j���̒����q���A�z�q���d�q�y�����j���[�g���m�ɕ���B
$n^{0} = p^{+} + e^{-} + \overline{\nu^{0}}$�����$\beta^{-}$����Ƃ����A�����q���z�q�ɕς�錻�ۂł���B�i���̋L���͓d�ׂ�\���B�j
���ɁA�z�q�ߏ�̌��q�j�ł́A�j���̗z�q���A�����q���z�d�q�y�уj���[�g���m�ɕ���B
$p^{+} = n^{0} + \overline{e^{+}} + \nu^{0}$�����$\beta^{+}$����Ƃ����A�z�q�������q�ɕς�錻�ۂł���B�i�I�[�o�[���C���́A�����q��\���B�j
���ӂP
���R�E�ɑ��݂��錴�q�j�́A�����q���z�q�Ɠ��������A�܂��͑����B���������Č��ۓI�ɂ́A$\beta^{-}$����̕���$\beta^{+}$�����舳�|�I�ɑ����B�܂��A�⑫�ŏ������悤�ɁA���̒����q�͎��R��$\beta^{-}$������N�������߁A�x�[�^����Ƃ����ƁA$\beta^{-}$����̂��Ƃ��Ǝv���Ă��邢��l�������B���̋@���$\beta^{+}$������o���Ă����Ƃ悢�B
���ӂQ
���̍��ł́A�z�d�q�E�j���[�g���m�y�є��j���[�g���m�A�X�ɒ��Ԏq�܂ł����o�ꂵ�����A���̍��ł́A�Ƃ肠�����A����Ȃ��̂�����A�Ƃ����F�����Ă��炢�����B�ڍׂ͕ʓr��������B
���āA�O��ނ̊j�͓͂���ł��邱�Ƃ����������B�Ƃ���A�u$p-p$�ԗ́v�����A�d���C�́i�˗́j����������̂ŁA�j�q�̌��т����s����ɂȂ�B�����A���q�j�̐����i���f�j���A$p$�̐��Ō��܂�Ȃ�A$p$�����łȂ��A$n$���������������q�j�͈���ɂȂ�̂ł���B�i$p$��$p$�̊Ԃɓ����āA$p$��$p$�̊Ԃɋ���������ڂƎv���悢�B�j�]���āA���q�j�ɂ͒����q�����݂��Ă悢�̂ł���B
�ŏ��́A�x�[�^������N�����͂��j�͂ł���A�ƍl����ꂽ�������������B�܂茴�q�j���ŁA$p$��$n$�ɁA$n$��$p$�ɕϊ����邱�Ƃɂ��A�����Ɉ��͂����܂��A�Ƃ����_�@���B��������闱�q�́A�d�q�i�z�d�q�j�Ɣ��j���[�g���m�i�j���[�g���m�j�ł���B�������A�^����������B����́A�������Ă��闱�q���A�o���ňقȂ邱�Ƃ��B
����ɁA���̃x�[�^����ɂ�茻���͂��v�Z���Ă݂�ƁA�d���C�͂�肸���Ə��������Ƃ����������̂��B���̗͂ł͊j�q���܂Ƃ߂邱�Ƃ͑S���s�\�������̂ł���B
���Ƃ���A���̃x�[�^����Ƃ������ۂ́A�����������Ȃ̂��Ƃ����^�₪�N���B�������A�����̗͂ł��邱�Ƃ͊m���ł���A���̗͂��u�ア�́i���ݍ�p�j�v�Ɩ��t�����邱�ƂɂȂ����B
�i���q�Ԃɓ����́A�Ƃ�������j�q�̕���𑣂����Ƃ��Č����̂ŁA�ア���ݍ�p�Ƃ��Ă��̂ł���B�j
����ŁA�������͎��R�E�̂S�̗͂�m�����B
�i�P�j�d���ł���B
�i�Q�j�d���C��
�i�R�j�j��
�i�S�j�ア�́i���ݍ�p�j
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�R�D���Ԏq
���āA�O���܂łɏo�Ă����f���q�����Ă������B
�i�P�j���q�i�d���C����}��闱�q�j�ʎq�_�I�ȏ��ł́A�͂̓����Ƃ���ɂ́A�����}��闱�q�����݁i�ߐڗ��j����A�Ƃ������ƂɂȂ��Ă���B
�i�Q�j�d�͎q�i�d����}��闱�q�j
�i�R�j�d�q�i���d���������A���q�j���ӂɑ��݂��A���q���\�����闱�q�j
�i�S�j�z�d�q�i�d�q�ƁA�d�ׂ̕����������قȂ闱�q�j
�i�T�j�z�q�i���d�ׂ������A���q�j���\�����闱�q�j
�i�U�j�����q�i�d�ׂ��������A���q�j���\�����闱�q�j
�i�V�j���j���[�g���m�i$\beta^{-}$����ŁA�d�q�Ƌ��Ɍ���闱�q�j
�i�W�j�j���[�g���m�i$\beta^{+}$����ŁA�z�d�q�Ƌ��Ɍ���闱�q�j
�i�X�j���Ԏq�i�j����}��闱�q�j
�d���C�́i�N�[�������j�́A���q���L���b�`�{�[���ɂ�蔭������B
�d�͂́A�������̗��q�ł����d�͎q�i�O���r�g���j�̃L���b�`�{�[���ɂ�蔭������i�ƍl�����Ă���j�B
�ア���i�x�[�^�����j�́A���ʉ����}��i�H�j���Ă��邩�s���ł���B
����ł́A�j�͂�}��闱�q�͉����H
�{�����t���C���O�Ȃ̂����A�O���Ŗ��O���������Ă��܂����B
����G�����m�́A���̗��q���������v�Z�ŋ��߁A�d�q���j�q�̒��Ԃ��炢�i�d�q��$200$�{���j�ł���Ɨ\�����A����Ɂu���Ԏq�v�Ƃ�������t�����B����āA�j�͂Ƃ́A���Ԏq��ł���A�Ƃ������ƂɂȂ����B
�]�k
���́A����́u���Ԏq�_�v�͔��ɕ]�������������B���R�́A���m�̗��q�����肷��A�ǂ�Ȏ��R���ۂł������ł��Ă��܂��A�Ƃ������Ƃ���ł���B�X�ɁA���Ԏq�����̌��ɂȂ�u�Ȃɂ��v�������ł��Ă��Ȃ����Ƃ����R�̂ЂƂ�������������Ȃ��B
�ʎq�_��Ă̐e�ŗL�����{�[�A�����������Ƃ��A�M�S�ɒ��Ԏq�_���������ɑ��A�u�N�́A����ȂɐV�������q���D�����B�v�Ɨ��₩�Ɍ������A�Ƃ����b�͗L�����B
�܂��A�i�{�����ǂ������m�F�̉\�ł��邪�j����Ɠ����悤�ɒ��Ԏq�_���v�������V���e�B�P���x���N�Ƃ����w���́A�搶�ł����p�E���ɁA�u��������܂���������Ƃ����āA����ȗ��q�����肷�����Ȃ��B�v�ƁA�_�����p������Ă��܂����Ƃ����b������B
�b�x��
�Ƃɂ����A���]�Ȑ܂͂��������̂́A����F�����̊ϑ��ɂ��A���́u���Ԏq�v�͔�������A���ʂ��d�q��$260$�{���x�ł��邱�Ƃ��m�F����A�j�͂�}��闱�q�Ƃ��ĔF�߂�ꂽ�B�i���Ԏq�_�́A�P�X�R�T�N�ɔ��\����A���Ԏq�̊m�F�͂P�X�S�V�N�������B�j
�t�������Ă����ƁA���Ԏq���j�͂�}���͈͂͋ɂ߂ď������i���ꂪ�A�������q�j�̑傫���ɂȂ�j�A���̗͂̑傫���͓d���C�͂�$100$�{�ł���B���̂��߁A���q�j�͋ɂ߂ď����ȗ̈�ɂ������݂ł��Ȃ��B
�����ŁA�{���́A�I�グ�ɂ��Ă������A�u�j�͂������錳�ɂȂ�ʁv�̘b�����Ȃ���Ȃ�Ȃ��̂ł��邪�A���闝�R�ɂ���A���̐����͍��̒i�K�ł͂ł��Ȃ��B���̘b�́u�펯�ҁv�łȂ��Ƃł��Ȃ����R������B�i�m���Ă���l�́A�b�������āA�����������Ă��邩������Ȃ����A�l�^�o���͍T����B���̂ɂ͏����Ƃ������̂�����B�j
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�S�D�ア��
�O���ł́u�ア���i�x�[�^�����������N�����́j�́A���ʉ����}��i�H�j���Ă��邩�s���ł���v�Ə������B
�d���ɑ��ẮA�i�������ł͂��邪�j�d�͎q�i�O���r�g���j������B
�d���C����}���̂́A���q�i�t�H�g���j�ł���B
�����āA�j����}���̂��A�O���Ő����������Ԏq�Ȃ̂ł������B
����ł́A�u�ア���v�͉����}���̂��H�@���������A�ア�͂́A���������������ē����͂ȂH�@�Ƃ����^��͓��R�ł���B
���́A�u�ア�́v�́A�j�q���u�E�B�[�N�{�\���v�Ƃ������q�Ƒ��ݍ�p����̂ł���B
����������ƁA�E�B�[�N�{�\�����ɂ����āA���z�E�B�[�N�{�\�����A�j�q�����ݍ�p����ƁA�j�q�̕ϊ��i�����q���z�q�ɁA�z�q�𒆐��q�Ɂj���N�����A���z�E�B�[�N�{�\�������̉����A�ɒZ���Ԃ��d�q���j���[�g���m�ɕ���̂ł���B�i���ǂݕԂ��Ȃ��ƁA������Ȃ��Ǝv���B�j
���܂łɓo�ꂵ�āA�����ł��Ă����d�������A�E�B�[�N�{�\����ɒu�������čl���Ă݂�B
�j�q�́A���z�E�B�[�N�{�\�����o������A�z�����肵�Ă���B�i������ċz����A�ƕ\������B�j
�����ċz���Ă��邾���Ȃ牽���N����Ȃ����A���܂��܂͂��o�������z�E�B�[�N�{�\����ʂ̗��q���߂܂��Ă��܂��ƁA���̗��q�Ԃɗ͂������B���ꂪ�u�ア�́v�ł���B�@�����܂ł͂悢�B�������A���̐悪���܂������ł��Ȃ��Ȃ�B
�Ⴆ�A�d����ł́A
�d�ׂ����������q�����z���q���L���b�`�{�[���@���@���q�ԂɈ��́E�˗͂������ƕ\���ł���B
������ア�͂ɂ��Ă͂߂Ă݂��
���炩�̉חʂ����������q�����z�E�B�[�N�{�\�����L���b�`�{�[���@���@�����������Ȃ��i�����Č����Ȃ痱�q���ϐg����j�Ƃ������ƂɂȂ��Ă���B
�N�����Ă���̂̓x�[�^���B�u�ア�́v�ƃx�[�^������Ȃ������͉��Ȃ̂��A�����l�������Ȃ��́A�Ƃ��Ă��܂Ƃ��ł���B�@�����ŁA���ꂩ�炻����������B
�N���肤�錻�ۂ̎�ނ́A
�@�i�P�j�z�q���͂��o�������z�E�B�[�N�{�\����z�q���߂܂����ꍇ
�@�i�Q�j�z�q���͂��o�������z�E�B�[�N�{�\���𒆐��q���߂܂����ꍇ
�@�i�R�j�����q���͂��o�������z�E�B�[�N�{�\���𒆐��q���߂܂����ꍇ
�@�i�S�j�����q���͂��o�������z�E�B�[�N�{�\����z�q���߂܂����ꍇ
�ȏ�A�S�ʂ肪�l������B�i�٘_�͂���܂���ˁB�j
�����S���Ђ�����߂Đ������邽�߂ɂ́A���z�E�B�[�N�{�\���Ƃ́A�j�q�ԂɁA���́E�˗͂������炷�̂ł͂Ȃ��āA�z�����j�q��ϐg�������ƍl���Ȃ���Ȃ�Ȃ��B
���A���z�E�B�[�N�{�\�������Ɂi$W$�j�ŕ\������ƁA��L�i�P�j�̃P�[�X�ł́A
$p + p �� (p + W) + p �� p + (p + W) �� p + ( n + e^{+} + \nu)$��P���F��̗z�q��������
��Q���F�Е��̗z�q�����z�E�B�[�N�{�\������o����
��R���F��������̗z�q�����z�E�B�[�N�{�\����߂܂���
��S���F���̌��ʁA�z�q�̓x�[�^����i��+�j���N�����A�����q�ɕς����
�S���̍�����A���́i$p$�j������Ă��܂��A
$p �� W + p �� p + W �� n + e^{+} + \nu$�ƂȂ��āA����́A$\beta^{+}$���̂��̂��B�������z�E�B�[�N�{�\�����ǂ�����Ƃ��Ȃ��o�ꂵ���`�ɂȂ��Ă���B
���l�Ɂi�Q�j�`�i�S�j���l���Ă݂�B
�i�Q�j
$p + n �� (p + W) + n �� p + (n + W) �� n + (p + e^{-} + \overline{\nu})$�i�R�j
$n �� W + n �� n + W �� p + e^{-} + \overline{\nu}$
$n + n �� (n + W) + n �� n + (n + W) �� n + (p + e^{-} + \overline{\nu})$�i�S�j
$n �� W + n �� n + W �� p + e^{-} + \overline{\nu}$
$n + p �� (n + W) + p �� n + (p + W) �� n + (p + e^{+} + \nu)$���ʓI�ɂ́A�ŏ��ɉ��z�E�B�[�N�{�\�����͂��o�����j�q�ɊW�Ȃ��A���z�E�B�[�N�{�\�����z�����j�q�̕��ς�邾���Ȃ̂ŁA�i�P�j�Ɓi�S�j�A�i�Q�j�Ɓi�R�j�͓������̂ł��邱�Ƃ�������B��������B
$p �� W + p �� p + W �� n + e^{+} + \nu$
�@$\beta^{+}$����
$p + W �� n + e^{+} + \nu$�A$\beta^{-}$����
$n + W �� p + e^{-} + \overline{\nu}$���_�A���z�E�B�[�N�{�\���́A�j�q���x�[�^�������B���̂��Ƃ͂Ȃ��A���ꂪ�u�ア�́i���ݍ�p�j�v�ł���B
�����āA���̃E�B�[�N�{�\���������錳�ɂȂ�ʂ��u��ׁi�E�B�[�N�ׁj�v�Ƃ����B�Ȃ���Ⴀ�A�Ǝv���l�͐���ŁA�����g���̖��O�̕t�����͂��܂�ɂ������ł���A�Ƃ�����Ă���B
����������Ă���̂́A�u�j�q�v�Ɓu�d�q�v�Ɓu�j���[�g���m�v�i�x�[�^���̂܂�܂ł���j�Ƃ������ƂɂȂ�A�E�B�[�N�{�\����ł́A�j�q���x�[�^����̂ł���B
�����l���Ă���ƁA����Ȃ��ƂɋC�Â��B����́A�Ⴆ�A��������̊j�q�������ł͂��o�������z�E�B�[�N�{�\���������Ōċz���Ă��x�[�^�����Ȃ����A�Ƃ������Ƃł���B
�����A���̋^������Ă���A�����A���̋^�₾���ŁA�����f���q�_�̒P�ʂ����炦��B
���ۂɂ���͋N���Ă���B�O�ɏ������͂����B�u���̒����q�́A�����Ă����ƁA$\beta^{-}$���āA�z�q�ɕς��v�ƁB
����́A�܂��Ɏ������g�����o�����E�B�[�N�{�\���Łu�ア���ݍ�p�v�����Ă���̂ł���B
���Ⴀ�A�Ȃ�ŗ��̗z�q�́A�����q�ɂȂ炢�H�@�Ƃ����^�₪�ł��s���w�E�Ȃ̂��B����́A�ƂĂ��Ȃ��䂾�����̂ł���B�C����������悤�ň������A���̉́A�w�킩��܂őf���q�_�u�펯�ҁv�x�ŏ������Ƃɂ���B�i�[�����R������̂ŁA�����Ă��������B�j
����ŁA�S�̗͂����̎p�m�Ɍ������B
�i�P�j�d���i�d�͎q���}��j�A���A���̂��Ƃ��m�F���Ă����Ȃ���Ȃ�Ȃ��B
�i�Q�j�d���C���i���q���}��j
�i�R�j�ア���i�E�B�[�N�{�\�����}��j
�i�S�j�j���i���Ԏq���}��j
�i�P�j�d�͂́A�u�����v�������q�Ԃɓ���
�i�Q�j�d���C�͂́A�u�d���v�������q�Ԃɓ���
�i�R�j�ア�͂́A�u����v�������q�Ԃɓ���
�i�S�j�j�͂́A�u�H���v�������q�Ԃɓ����i�����_�ł͕s���j
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�T�D�t�@�C���}���E�_�C�A�O����
�O���ł́A�ア�����������q�Ƃ��̎d�g�݂͂Ǝ������Ő��������̂ŁA�ǎҏ����ɂ͍��������������̂Ɛ��@����B
���ۂɕ����w�ҒB���A�f���q�_�i��̗ʎq�_�ƌ��������Ă������j�ɂ����ẮA�N�����Ă��邱�Ƃ��I�ɗ�������̂ɋ�J�������j������̂ł���B
�č��ɁA���`���[�h�E�t�B���b�v�X�E�t�@�C���}���Ƃ��������w�҂������B�P�X�W�W�N�ɖS���Ȃ��Ă���̂����A���̑�w����̋��ȏ��́u�t�@�C���}�������w�v�������B���̋��ȏ��̂����b�ɂȂ����l�͑����̂ł͂Ȃ����Ǝv���B�ނ́A�P�X�U�T�N�ɓ��{�����i�U��Y���A�č����W�����A���ES�E�V���C���K�[���ƂƂ��ɁA�ʎq�d���C�w�̕�����m�[�x�������w������܂���ȂǗl�X�Ȍ��т�����̂����A�ł��L���Ȃ̂��A�{���Ŏ��グ��u�t�@�C���}���}�i�_�C�A�O�����j�v�ł���B
�t�@�C���}���}�Ƃ͉����������Ő������邱�Ƃ́A�t�@�C���}�����Ɏ���ł���B�Ȃɂ��땨���w�����o�I�ɕ\������\�͂ł͉E�ɏo����̂����Ȃ��ƌ���ꂽ���Ȃ̂�����A�����͐��������ŁA�t�@�C���}���}�����Ă��炨���B

��}�́A���f���q�i�z�q���d�q�j�ɂ������d���C�́i�d�����ݍ�p�j��\�����t�@�C���}���}�ł���B���������[���������āA����𗝉�����Η��q�����ݍ�p����ڗđR�Ɍ��Ď�邱�Ƃ��ł���D����̂ł���B
�����́A�������q�i�z�q�A�����q�A�d�q�Ȃǁj��\���B�g���͗͂�}��闱�q�i���q�A�E�B�[�N�{�\���Ȃǁj�������B�����ɂ͖���Ă���̂ŁA�ω������邱�Ƃ��ł���B
�T�ˁA���̂��炢�𗝉�����A�������Ă킩��͂��ł���B
�E���ɗz�q�i$p$�j�������āA�����ɂ͓d�q�i$e^{-}$�j������B�z�q���d�q���ω����Ȃ��̂����A�g���̌��q�i$\gamma$�j���o�Ă���Ƃ���Ő܂�Ȃ����Ă��Ē��_���ł��Ă���B�����ŗ͂��`����Ă���ƌ���悢�̂ł���B
�z�q�i$p^{+}$�j�Ɠd�q�i$e^{-}$�j�̊Ԃ����q�i$\gamma$�j���s�������āA�N�[�����͂��������Ă��邱�Ƃ������Ă���B
�P�ɗ͂��`��邾���Ȃ�A�d�����A�j���������_�C�A�O�����Ŏ������Ƃ��ł���̂����A���́u�ア�́i���ݍ�p�j�v�ł���B
���̐}�����Ă��炢�����B

�����ɂ͒����q�i$n$�j������A�E�B�[�N�{�\���i$W$�j����āA�����q�i$n$�j���z�q�i$p$�j�ɕω����Ă���B�����āA�E�B�[�N�{�\���i$W$�j�͕��o��ŁA�d�q�i$e^{-}$�j�Ɣ��j���[�g���m�i$\overline{\nu}$�j�ɕ��Ă���B
���ꂪ�܂���$\beta^{-}$�����Ȃ̂ł���B
���̂��Ƃ��A�@�����t�@�C���}���}��p���āA��������Ղ����čs������ł���B
�ꌾ���������I

�y�킩��܂őf���q�_�u����ҁv�@��Q�́@�S�̗́z
�ڎ����@�@���i���@�@�O�֖߂�
�U�D���Ԏq�̎���
�j�������Ԏq���`����Ƃ������ƂŘb�����Ă����B���������O���ŏo�Ă����t�@�C���}���}���g���Ċj�͂��݂Ă݂悤�B�����Œ��Ԏq��$\pi$�ŕ\�����Ƃɂ���B

��}�́A�����q�i$n$�j���z�q�i$p$�j�����т��ۂ̃t�@�C���}���}�ł��邪�A�z�q�|�z�q�A�����q�|�����q�ł����Ă��͓����ł���B���Ԏq���L���b�`�{�[�����Ă��A�z�q�A�����q�͕ω����Ȃ��B���������āA���Ԏq���d���[���ł���B
�������A���Ԏq�ɓd�ׂ����������̂�����Ƃ���ƁA�ȉ��̂悤�ȑ��ݍ�p���l���邱�Ƃ��ł���B


�d�ׂ����������Ԏq���L���b�`�{�[������ƁA�z�q�������q�ɁA�����q���z�q�ɕς��̂ł���B�����A�ǂ̏ꍇ�ł����q�j���̗z�q�A�����q�̐����ω����Ȃ��̂ŎO�̂����̂ǂꂪ�N�����Ă���̂�����ʂ���Ӗ����Ȃ��B
�x�[�^�����i�ア���ݍ�p�j�̗��_�́A�t�F���~�ɂ���č��ꂽ���A�����͂܂��ア�͂�}��闱�q�Ƃ������z���Ȃ������̂ŁA�P���ɒ����q���z�q�Ɠd�q�����j���[�g���m�ɕ�����̂��ƍl�����Ă����i�E�B�[�N�{�\�����o�ꂷ��̂́A��̗ʎq�_�����W���Ă䂭�P�X�V�O�N��ł���j�B
�����͒��Ԏq�_�\�����Ƃ��ɁA�x�[�^����ɑ��āA���̂悤�ȉ��߂������Ă����悤�ł���B

�܂�A���o�������Ԏq��߂܂��鑊�肪���Ȃ��ƁA���Ԏq���d�q�Ɣ��j���[�g���m�ɕ��ăx�[�^���N����Ƃ����}�����B
���̃A�C�f�A�͎��ۂɂ͂��܂��䂩�Ȃ��������A��̏�̗ʎq�_�ɂȂ�����тƂ��ĕ]������Ă���B
��������{���̖{��ɓ���B
�����������삪�j�͂�}��闱�q�ɒ��Ԏq�Ƃ������O��^�����̂́A���̗��q���A�j�q�Ɠd�q�̒��Ԃ��炢�����������ƌ��_�t�������炾�B�{���ł́A���̗��R��������Ɛ������Ă������B
�j�͂��d���C���̑傫�ȈႢ�́A�͂������������S���قȂ�_���B���������錴�q�j���̊j�q�������ȊO�̕ʂ����q�̌��q�j�ɓ����قǂ̗͂ł�������A���q���m���j�͂ł������Ă��܂��A�����������̂悤�Ȏ��R�E�͑��݂��Ȃ��Ȃ��Ă��܂��B�]���āA�j�͂Ƃ́A���q�j�̑傫�����x�̗̈�ł��������Ȃ��悤�ȗ��Ȃ̂ł���B�i���͈̔͂Ƃ́A$10^{-15}m$�Ƃ����l�ł���B�j
����ɑ��āA�d���C�͂͌��Ⴂ�ɍL���͈͂ɓ����B���q�j�Ƃ��̎���̓d�q���֓��̒n�}�ŕ\�����}���v���o���Ăق����B�j�͂������͈͂������w�ɂ����ꂽ$1m$�̃{�[���ł���Ƃ�����A���̌��q�j�Ɠd�q�̊Ԃɓ����d���C�͂́A�֓���~�ɍL����قǑ傫���i���ۂɂ͓d���C�͂́A�����ɔ���Ⴕ�Ďキ�͂Ȃ邪�A�����I�ɂ͖����̉����܂œ`���͂Ȃ̂ł���j�B
����́A�͂�}��闱�q�̎��ʂɊW����B
���ɏq�ׂ��悤�ɁA�j�͂�}��钆�Ԏq�́A���q�j�͈̔͂ɂ������邱�Ƃ��ł��Ȃ��B����́A���Ԏq�����݂��Ă����鎞�Ԃ��ɒ[�ɒZ�����Ƃ��Ӗ����Ă���B
���������A�j�q�i�z�q�A�����q�j�����Ԏq����o����̂́A�G�l���M�[�ۑ����Ɉᔽ�����B���ʂ̓G�l���M�[�Ɠ����i$E=mc^{2}$�j�Ȃ̂�����A���Ԏq�̕��o�́A������G�l���M�[�ݏo�����ƂɂȂ�B
�Ƃ��낪�A������G�l���M�[�����܂�Ă��悢�Ƃ����P�[�X���������͂��ł���B���ꂪ�A�u���ԁv�Ɓu�G�l���M�[�v���s�m�萫�����ł���B�i�ڍׂ́A�u�Ȃɂ͂��Ă����ʎq�_�v�Q�Ɓj
$\Delta{t} \times \Delta{E} \geqq h/4 \pi$$\Delta{t}$��$\Delta{E}$���|���Z�������̂�$h/4\pi$��菬�����͂Ȃ�Ȃ��̂�����A�����ł́A
$\Delta{t}$�F���Ԃ̕s�m��i���̏�āA���Ԏq�����݂��Ă��������ԁj
$\Delta{E}$�F�G�l���M�[�̕s�m��i���̏ꍇ�́A���Ԏq�̎���$ \times ����^{2}=mc^{2}$�j
$h$�F�v�����N�萔�i$6.6207015 \times 10^{-34} Js$�j�� $h/{4 \pi} = 0.5268586852 \times 10^{-34}$
$\Delta{t} \times \Delta{E}=h/4 \pi$�Ƃ���B
$\Delta{t}$�̍ŏ��l�͌��߂邱�Ƃ��ł���B�܂�A���Ԏq�����̐��̍ō����x�ł�������i$c$�j�ŁA���q�j���i$s=10^{-15}m$�j��[����[�܂ő��鎞�Ԃł���B
����ŁA
$\Delta{t}=s/c$�Ƃ������Ƃ��ł���
$\Delta{E}=mc^{2}$
$\Delta{t} \times \Delta{E} = s/c \times mc^{2} = smc = h/4 \pi$�ƂȂ�B �����
$m = (h/4 \pi) /sc$�ŁA���Ԏq�̎��ʂ����߂邱�Ƃ��ł���B��̓I�ɒl��������� \begin{eqnarray} m &=& 0.5268586852 \times 10^{-34} / ( 10^{-15} \times 299792458)\\ &=& 1.75883747 \times 10^{-29} \end{eqnarray} �ƂȂ��āA�d�q�̎��ʁi$9.1093837 \times 10^{-31}kg$�j�Ɣ�r����Ɩ�$193�{$�ƂȂ�̂ł���B
���Ԏq���j�q�Ɗj�q�̑��ݍ�p��S���i�j�͂�}���j���߂ɂ́A�Œ�ł����ꂾ���̎��ʂ��ǂ����Ă��K�v�ɂȂ�̂ł���B
���͂��@�@�ꌾ���������I
