【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

沖田十三
1.波動関数
量子論において有名な「猫」の話をするには、前置きが必要で、しかも長い。しかし、みなさんはしっかりその前置きに耐え、無事「猫」の問題にたどり着けることを信じて疑わない。
まず、第一の前置きであるが、「波動関数」である。(あっ、ここで読むのを止めようとした人がいるでしょう。ダメです!ちょっと付き合ってください。)
最初から余談
「宇宙戦艦ヤマト」は、『波動砲』なる必殺技を持っている。これを一発ぶっ放すと、全てが解決するという夢のような武器である。あたかも、ウルトラマンのスペシウム光線のようだ。(歳がばれますね、こんな話をしていると。)
『波動砲』とは、いったいいかなる「波動」を発射しているのだろうか? 影像によれば、ヤマトのエネルギー充填状態が$120\%$になると、艦長”沖田十三”が、「発射!」と叫ぶ。するとヤマトの艦前方に開いた穴から、炎のような束が前方に発射され、多くの場合、その束を浴びた物は、熔けるように爆破消滅してしまうのであった。
もし、波動が電磁波だったら、多分こんなことは起きない。高エネルギー電磁波(ガンマ線)の位相を合わせて、レーザーにしても、それを浴びた物体をレーザーが貫通したり、すぱっと切れることはあっても、熔け爆発することはないはずである。いったいあれは何の波動なのだろう? 疑問は尽きない。
閑話休題
波動関数とは、粒子の状態を数式で表したものである。
なんかおかしいと感じた人が必ずいると思う。
波動関数なのに、粒子? という疑問である。この「量子論」の話では、再三「物質は粒子であり、波である」と繰り返してきたのであった。だから、とりあえず、一番最初に言い訳をしておく。
そして、もうひとつ、
波動関数は、他の物理関数のように、時間と位置を変数とする関数になっている。そしてこの関数はギリシャ文字のプサイ$(\psi)$で表す慣習になっている。
空間を何の束縛も受けず自由に直線運動をしている粒子の波動関数は、次のように表される。
説明しなくてもおわかりと思うが、$(\cos)$はコサイン、$(\sin)$はサインを表す。
説明しなくてもおわかりと思うが、$(i)$は虚数単位$\sqrt{-1}$を表す。
説明しないとわからないと思うが、$(A)$は波の振幅である。
説明しないとわからないと思うが、$(\omega)$は$(2\pi\nu)$である($\nu$は、ご承知の通り振動数である)。
説明しないとわからないと思うが、$(k)$は$(2\frac{\pi}{\lambda})$である($\lambda$は、ご承知の通り波長である)。
振動数$(\nu)$は、粒子のエネルギーに関係している。($E=h\nu$を思いだして!)
波長$(\lambda)$は、粒子の運動量に関係している。($p=\frac{E}{v}=\frac{h\nu}{v}=\frac{h(\frac{v}{\lambda})}{v}=\frac{h}{\lambda}$)
つまり波動関数は、物質の粒子としての側面と波動としての側面を全て持った関数である、ということが言える。
ここで、思考実験をする。今、上記で表される粒子と同じ速度で粒子と同じ方向に走っているとする。すると、コサイン、サインで表される正弦波は形を変えないはずである。そのはずである。
従って、
つまり時間と共に粒子は位置を変える、つまり静止してはいられない。これが、とりあえずの結論。
つまり、粒子であろうとも絶対に静止できない、これは、「不確定性原理」そのものである。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る
M.ボルン
2.幽霊波
前回、「空間を何の束縛も受けず自由に直線運動をしている粒子」の波動関数を説明した。それがきちんと理解できたか否かは大きな問題ではない。
状況によって、波動関数は様々な状態に変化しうる。前項のような単純(どこが単純じゃ!と思うかも知れないが)でない場合も多々ある。ただ最も単純な状況であっても、波動関数に、虚数項が入っていることに注目してもらいたい。
数式に虚数が現れる(複素関数である)と、物理では、それは「観測不能」であるということと同じ意味と捉える。その話を今回しようと思うわけであるが、この時点で意味を理解している人はいないはずである。具体例で話をする。
以前、ド・ブロイが「電子は波である」ことを提唱し、それが実験的に確認された、という話をした。
その実験とは、電子線を蛍光面へビーム状に発射するとき、電子源と蛍光面の間にスリットを置く、という簡単な実験である。
何のことだか理解不能という人は、まず図10−1をみてもらいたい。
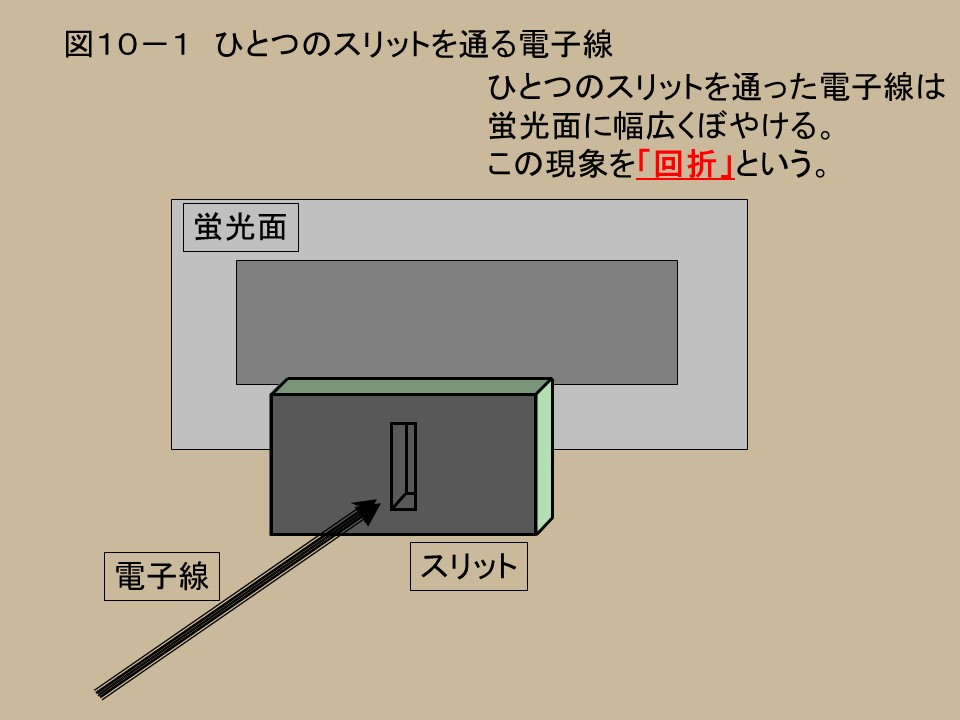
ひとつ穴のスリットを通った電子線は、蛍光面に幅広くぼやけた像を結ぶ。この現象は、光でよく知られており、「回折」というものである。
次に、図10−2を見てもらいたい。
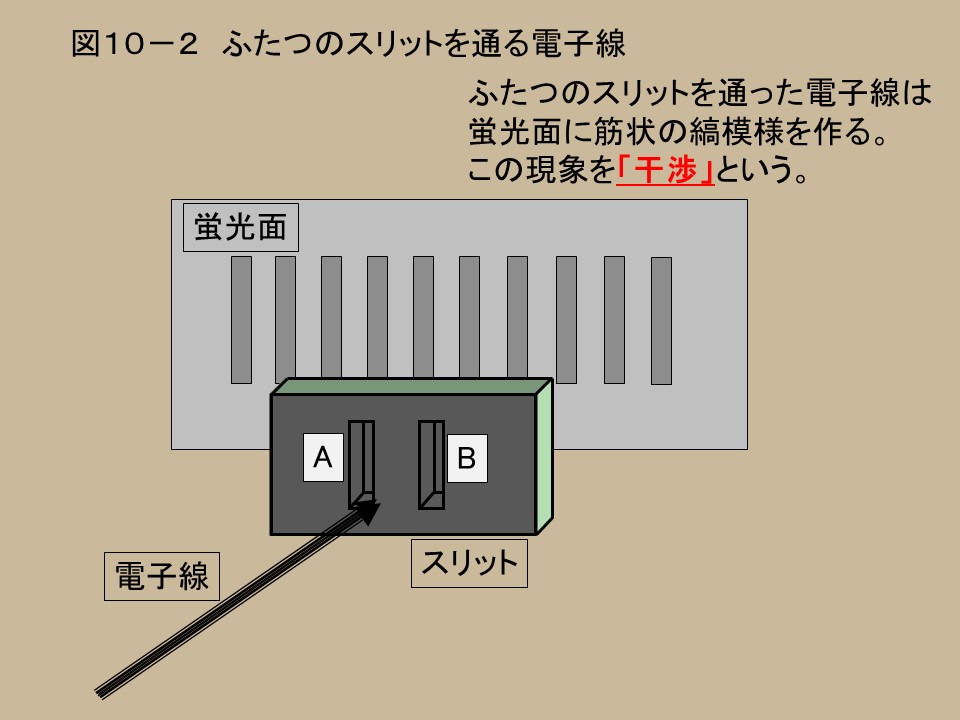
ふたつ穴のスリットを通った電子線は、蛍光面に筋状の縞模様を作る。この現象は、「干渉」と呼ばれる。
どちらも、波でなければ起こらない現象であり、ド・ブロイの電子波は、これらの実験で証明された。
ところで、この波動関数に物理的な解釈を求めたのがドイツの”ボルン”である。
後者の二重スリットの実験において、電子という一個の粒子は、スリットAか、スリットBのどちらかを通るはずであり、スリットの近くに検出装置を置いて観測すれば、どちらを通ったかを検出することができる(はずである)。従って、電子のとる状態は二種類あることになる。
電子が二重スリットのどちらを通過したのかは、観測してみなければ解らないので、観測されない状態で、電子の状態を書き表せば、波動関数は、上記両者の重ね合わせとして、
ただし、この重ね合わせの式は、たった一個の電子についてのものであることに注意してもらいたい。波動関数、$(\Psi)$や$(\psi)$は、複素関数なので、実在する波を表しているのではなく、数学的な波である。
ボルンは、この波動関数の2乗、すなわち
どういうことかというと、波動関数$\psi(x)$を、電子が位置$(x)$にいる時の波動関数と考えれば、$|\psi|^2$は、電子が位置$(x)$に存在する確率であるということだ。
なぜ波動関数の2乗が出てくるかというと、2乗することにより虚数項が消えるからである。絶対値の記号$(|△|)$が出てくるのは、結果を必ず正の数にするための細工である。
細工と言っては、ボルンに失礼だ。測定に掛からない波動関数に対し、測定可能な2乗項を「確率」と見抜いたボルンの慧眼は特筆すべきである。(教育者としても、数々の物理学者を育てたボルン、アインシュタインとの親交も深く、「神はサイコロを振らない」という名言は、アインシュタインがボルンに当てた書簡で述べられた。米国の歌手であるオリヴィア・ニュートン・ジョンの祖父でもある。)
波動関数を2乗することで現れるこの確率はあくまで、電子一個に対する確率である。
それでは、AとBの両方が開いているときは?
実はこれではよくない。なぜ? これだと、回折模様が重なるだけで、干渉縞が出てこないからだ。
そこで、実際のAとBの両方が開いているときの波動関数は、
さて、蛍光面へ発射する電子の数が膨大になれば、この確率は一般の確率分布に従い、その結果、図に示したような回折模様や、干渉縞が現れることになることは納得できる。これは実験的にも確かめられている。ところが、上式は、一個の電子の波動関数であるという。ならば、この関数を素直に解釈すれば、一個の電子が、スリットAもBも通ることになってしまう。
これをどのように見るか?
観測される前の電子は、波動関数という複素関数なので、その状態は「解らない」のだ。ただ言えるのは、その波動関数の2乗が、一個の電子が、Aを通るかBを通るかの確率の重ね合わせになることである。
理解が難しくなって来た。要するに、観測される前の電子の状態は、波動関数という幽霊波なのである。どうやったって解らないのである。これを言い換えると、電子を観測したとたん、電子は実在として現れるから、波動関数という幽霊は消滅する。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

A.アインシュタイン
3.波動関数は光速を超えて
おさらいをする。
「物体」を「波」と捉えている間は、その「物体」は何ものか解らないのだ。それは波動関数という名の幽霊波(複素関数)だからである。「物体」を「粒子」と認識した瞬間、波動関数が消えて、そこに粒子が現れる。
これが、前回言ったことだ。
だから、波動関数としての電子波がどこを通ってそこに現れたのか、誰にも(たとえラプラスの悪魔であっても)解らんのだ。よいか、だからラプラスの悪魔は存在できないことになってしまうのだ。
「誰にも認識できないものは、物理学で相手にしてはいけない、と何度も言ったよなあ。この場合はどうしてくれる!」と怒らないでほしい。前回をちゃんと読んでくれた人には、次の事実がわかっているはずだ。
たくさんの電子が二重スリットを通り抜けるとき、それらの総和は、電子が蛍光面のどこへ到達するか、という確率になる。それが干渉縞なのだ。
ところが、これを1個の粒子に当てはめるから話はややこしくなってくる。(もともと波動関数は、個々の粒子状態を表すものであり、大量の粒子線の分布確率を表すものではない。)
そこで今回は、次のような思考実験をする。
ちょっと唐突かもしれないが、粒子$A$があって、これが粒子$B$と粒子$C$に崩壊すると考える。$B$と$C$の質量に違いがないとし、崩壊した粒子$(B、C)$は共に粒子$A$がいた場所から飛び去るとすれば、もし$B$、$C$を粒子として考えれば、運動量が保存されるのだから、$C$は$B$と逆方向に飛んで行くはずである。ここまではよいだろうか。
ところが、$B$、$C$を波として見ると、$B$も$C$も、$A$のいた位置からあらゆる方向へ伝播して行く波動関数である。どこを飛んでいるか解らないのだ。幽霊波たる所以である。
しかし、ある場所で、$B$を「粒子」として観測したとする。この瞬間、Bの波動関数は消滅する。$B$が実態として現れる。とりあえずここまではよい。
ところが、粒子としての$C$は、粒子$B$と逆方向へ走っていることが解っているのだから、粒子$B$を観測した瞬間、$C$の波動関数も消滅し、粒子$C$が姿を現すことになる。これは困った。
何が困った?
粒子$A$があった場所から、粒子$B$が観測された地点までの距離を仮に、$10$光年とする。なにが起きるか、粒子$B$が観測された瞬間、粒子$C$の場所が判明するのだから、「粒子$B$が観測されてしまった。」という事実は、瞬間的に粒子$C$を実体化させる。このとき、$B$と$C$が、$20$光年離れているという距離は関係なくなってしまう。
「粒子$B$が観測されて波動関数が消滅する」=「粒子$C$が実体化する」のであれば、粒子$B$の波動関数消滅は、光速を超えて、粒子$C$を実体化させる。
この宇宙で、光速より速いものはない、という相対論に反してしまう。
もちろん、”アインシュタイン”は、このことに大反対し、次のように主張した。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る


N.ボーア A.アインシュタイン
4.異議あり!
物体とは、「粒子として観測されるまでは、2乗すると存在確率となる波動関数、という波である」というのがボルンの下した結論であった。
その結果の解釈として「波動関数の消滅」(これを「波束の収縮」と呼ぶのが一般的なので今後はこの言葉を用いる)という現象が、時間を要しない、すなわち光速度を超えるという解釈を”アインシュタイン”が許すはずがない。そこで彼は、量子論の根底である「不確定性原理」を否定することで、「光速度を超えるもの」を間違いであると言おうとした。つまり「時間とエネルギー」の不確定を否定する思考実験が登場したのである。有名な「ボーアとアインシュタインの論争」である。
さて、アインシュタインは反論した、のであるが、なにしろ電磁波という明確な波が実は粒子としての側面を持っている、と言い出したのは、誰あろうアインシュタイン本人である。
光電効果を思いだしてもらいたい。波長の長い電磁波をいかにがんがん当てても飛び出さない電子が、ある波長より短くなると、ほんの少しの照射で飛び出す、という現象が光電効果である。
プランクは、これを次の式で表せることに気付いた。
だが、波束の収縮をアインシュタインは認めなかった。次の言葉が有名だ。
アインシュタインは、実は全ては決定されている、というラプラスと同じ考えを持っていたのだ。つまり、粒子が観測された時、その粒子がたどってきた道のりは決まっているのだと考えた。それが現在の我々には示せないだけであると主張した。それは量子論がまだ不完全である証拠とまで言い切った。
今思えば、この点に関してはアインシュタインも実に保守的な物理学者であった。この意味で相対論ですら古典物理と言われるのである。
私は、アインシュタインが保守的な物理学者であったというよりは、あまりにも孤高の物理学者であろうとし過ぎたのではないかと考えている。特殊相対論と一般相対論を一人で創りあげ、晩年は、電磁波と重力を一本化する方法(大統一理論)に取り組んだほどの独立独歩の物理学者である。
ところが、量子論は一人では創れない、そういう理論であったことを証明したのが”ボーア”であった。コペンハーゲンに花開いた量子論は、彼が集めた若手物理学者達の群れから浮かび上がって来たものである。
粒子が量子として観測されるまでは、それが確率的にしか示せない存在である、というのが波動関数を不確定性原理に置き換えたものである。そして四元物理量の導入により、それが時間とエネルギーの不確定関係になる。言い換えれば、四次元時空間上の一点を占める粒子は、そのエネルギーも運動量も確率的に決定されるものであって、それ以上のなにものでもない、ということだ。
アインシュタインはこの「時間とエネルギー」の不確定を否定する思考実験をボーアに突きつけた。時に1927年のことである。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る
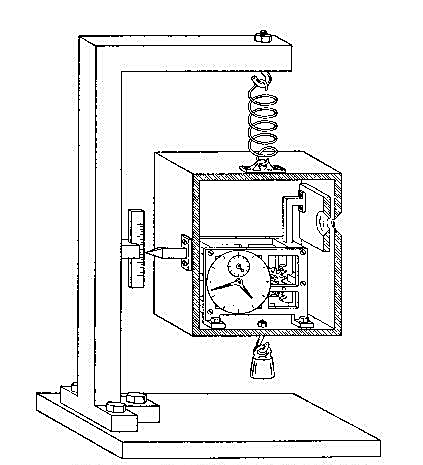
思考実験の図
5.思考の対決
アインシュタインが持ち出したのは、シャッターのついた箱をつるしたバネ秤であった。箱の中には、光という形でエネルギーが存在すると考える。シャッターを開けるとそこから光が飛びだす。アインシュタインはこの思考実験で次のように主張した。
(1)シャッターを開ける前の箱のエネルギーは、時間さえかければ好きなだけ正確に測定できる。
(2)箱のシャッターを開けて光(エネルギー)を放出する
(3)光を放出後のエネルギーも(1)同様好きなだけ正確に測定できる
(4)よって、放出されたエネルギーはいくらでも正確に測定できる。
(5)これは、光を放出した時間(シャッターを開けた時間)に依存しない。
(その気になれば、シャッターを開ける時間をいくらでも小さくできるのだから)
(6)よって、$(\Delta E=0)$でも$(\Delta t=0)$が可能である。
いかがであろうか。思考実験の創始者たるアインシュタインである。よく考えられたものだと感じないだろうか?
これには、ボーアも困ったらしい。一晩徹夜して答えを考えたと言われている。
なんとボーアの反論はアインシュタインの一般相対論を逆手に取った次のようなものである。
(1)バネ秤で、質量を正確に測るということは、バネの延びを前提としている
(2)バネが延びて箱が下がると、これが地球上では、前後で重力加速度が変わる
(3)重力加速度が変われば、時計の進みが変わるのは、一般相対論の結論である。
(4)よってバネの延びを限りなくゼロに近づけることが、時間を正確に測ることの条件である
(5)バネの延びが限りなくゼロに近づけば、質量(エネルギー)は測れない
以上の論理で、$(\Delta t)$と$(\Delta E)$の不確定性を、一般相対論を用いて反論したのである。
大方の意見は、ボーアの判定勝ちである。なんとなく論点がずれたところでの空中戦のような気がしないでもない。しかし不確定性原理は依然として健在であり、従って波動関数もまた生きている。
「波束の収縮についてきちんと説明できない理論は不完全だ。」もしかするとアインシュタインが言いたかったのもこの事だったのかもしれない。波動関数という数式をどのよういじくり回しても、波束の収縮に繋がる解は得られないのである。したがって、波束の収縮は未だに解明されていない謎、と言う人もいる。
しかし現実にはこの解釈は違う、と私は考えている。観測すると粒子が現れた。それならば、その前の事なんてどうでもいいではないか。これが波束の収縮に対する答えである。
さて、量子論の神髄が少しずつ見えてきた。シュレーディンガーの波動方程式の話をすれば、「猫」はすぐそこにいる。というよりも、ここまでの議論の中にも「猫」はチラチラ姿を現しているのだ。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

E.シュレーディンガー シャーロック・ホームズ
6.シュレーディンガーの波動方程式
おさらいをしておこう。(しつこい、と思うかもしれないが、何度言っても解ったようで解らない気分の人が多いはず)
時空間を走る、ある粒子について、アインシュタインはこう言った。
それは実在する粒子であって、隠れた秩序に従っている。ただ我々が完全な秩序を知らないだけだ。
ボーアは次のように言った。
それは、私の観測によって創造された実在体験なのだ。私が見るまでそれは存在しなかったのだ。
それでは、水素原子の周りの電子について考えてみよう。
古典物理では、長岡半太郎が予言したような惑星モデルで水素原子が説明される。すなわち、プラスの電気を持った原子核の周りをマイナスの電気を持った電子が回っているというモデルである。
ところが、ド・ブロイにより電子も波であることが提唱され、それが確認された。
電子も、それが観測されるまでは、波動関数で示される複素関数であった。これを数式化したのは、オーストリアの物理学者”シュレーディンガー”である。
写真を見てほしい。パイプに火を付けようとしているその姿は、シャーロック・ホームズの風貌そのものではないか。
大学で物理を始める前は、自然科学のみならず古典言語の文法や詩、そしてドイツの哲学者ショーペンハウエルを読みふけったそうである。後に「シュレーディンガーの猫」の思考実験を提示したのも、哲学書の影響であろうか。
そんな彼が示したのが、かの有名な「シュレーディンガーの波動方程式」である。
波として見たときの粒子は波動関数である。しかし波動関数そのものが単純な形で数式化されない場合は、時間および空間に関する微分方程式を解かないと、波動関数そのものが明確にならない。このときの波動関数を導く方程式を波動方程式という。シュレーディンガーは、電子波が満足すべき波動方程式があるとすれば、電子の粒子としての属性$(E=h\nu)$と波動としての属性$(p=\frac{h}{\lambda})$の双方を満足させる必要があると考えた。
その結果導かれたのが次の方程式である。
$U$は、ポテンシャルエネルギーを表し.... と煩わしい説明はしないから、安心してほしい。
但し、次のことだけは、確認しておいてほしいのである。
この方程式を解くと求められるのは$(\psi)$である。これは電子波(波動関数)である。つまり、シュレーディンガーの波動方程式を解くと、水素原子の周りの電子の波動関数を求めることができる。
電子の波動関数を2乗すると、存在確率が求められるのであるが、これを素直に受け止めると奇妙なことになる。
今まで電子が回っているだろう、と思われていた軌道で最も存在確率が高く、そこから外れるにつれ徐々に存在確率が小さくなって行く、まるで雲のように見える妙な図が描かれる。
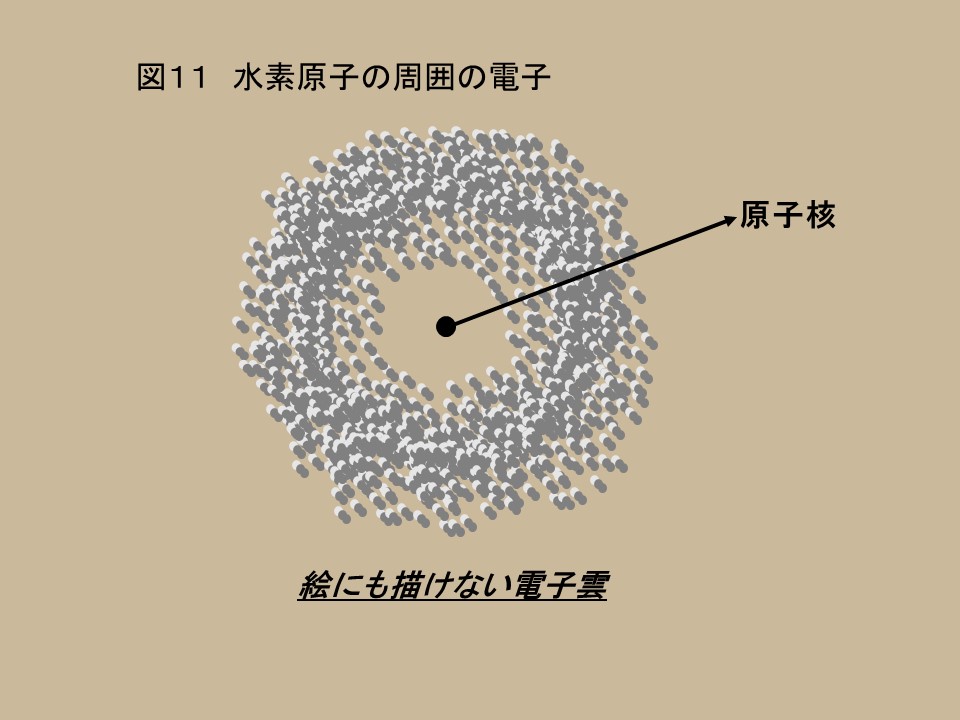
(実際の電子軌道は球面だから、本当はもっと絵にも描けないものである。)
しかも、この図が完全な電子の様子を示している訳ではない。あくまで、波動関数を$2$乗した確率分布が図のようになるだけなのである。
はいこの次は「猫」。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

シュレーディンガーの猫
7.「猫」の生死
シュレーディンガーの波動方程式から導かれる波動関数が、ある場合には水素原子の周りを回る電子の振る舞いを表すことは、前回までに述べた。その波動関数を2乗すると、前項で示した図のような電子雲で表現される存在確率の分布図として得られることも理解できたと思う。
電子の分布図は、次の二種類の解釈ができる。
さらに、霧のように観測される電子雲は、あくまで波動関数という複素関数の2乗である。実際には、霧のようなモノですらない。これを最終的にどのように捉えるかという問題は、シュレーディンガーの波動方程式が発表された時から存在した。
シュレーディンガー方程式から導かれる波動関数は、ある粒子のすべての状態の重ねあわせとして表現される。したがって水素原子の周りの電子は、原子核から無限に離れたところに存在するという状態、電子から一定の軌道上に存在する状態、原子核のごく近いところに存在する状態、・・・、というすべての場所に存在する場合の重ね合わせになる。
このとき、その状態の2乗をとってみると、「一定の軌道上に存在する状態」が一番大きくなるということが言えるのである。
この状況をもう少し単純化して提示してみよう。
ある粒子$A$が存在する。この粒子が$1$時間以内に崩壊する確率が$50\%$である、とする。これをどう見るか?
であるが、この粒子$A$を用いて次のような思考実験を行うとどうなるか。
動物愛護の観点から上記のような実験は許されない!と叫ばないでほしい。だから思考実験なのだ。
(a)の立場をとれば、猫が生きている確率は$50\%$である。
ところが、
(b)の立場をとれば、猫が生きている状態が$50\%$、死んでいる状態が$50\%$
というへんてこりんな状況が出現する。
(a)の立場をとる人は、こう主張する。
「猫は、生きているか、死んでいるかのどちらかである。その確立は五分五分だ」
(b)の立場をとる人の主張はこうである。
「猫は生きているという状態と死んでいるという状態を同じ程度に重ね合わせた状態だ」
勘違いしてはいけない、(b)の立場は、猫が半死半生であると言っているのではない。「明確に生きている猫」と「全く死んでいる猫」が重ね合わされた状態であるというのだ。
生きている状態と死んだ状態をどちらも持っている? そんな猫がいるのか?
それだけではない。覆いをとって「猫」の状態を見たとたんに、猫の状態は「生」か「死」に決定するということである。
なんだか話が解らなくなってきた?
でも量子論の神髄を当てはめると、上記のような状態が出現する。
覆いをとって、「猫」の状態を見るまでは、「猫は生きているし、死んでいる」という状態である。「生きているか、死んでいるかどちらかだが、その確率は五分五分だ」という状態とは明確に区別される。
アインシュタインは、上記(a)の立場をとり、「神様は、サイコロ遊びをしない」と言った。しかしボーアに代表されるコペンハーゲンで学んだ物理学者たちは、(b)の立場をとって「観測されるまでは、すべての状態の重ね合わせである」という立場になるのである。
つまり「猫の生と死」も波動関数という複素関数で表される波になってしまう。 どちらが正しいか?
明確な答えは、現在でも出ていない。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

デカルト
8.名問・珍解
実は、前項でこの章を終わるつもりだったが、なにか今ひとつ言い足りない気がしていた。そこへ絶好の質問をいただいたので、これに答えることで、「シュレーディンガーの猫」に対する補足説明としたい。
【質問】
なんで、シュレーディンガーが、件(くだん)の箱の中に生き物、それもねこなんて入れたのかは知りませんが、いつも違和感を覚えてしまうのはその部分です。
生きている状態と死んでいる状態の重ね合わせ、となったねこを想像できないんですよね。
言葉を介しての意思の疎通は出来ませんが、ねこにも意識があるだろうということはわかるわけで、だったら、自分が死んでしまったらそのことも多分わかるのではないかと思うわけで、ねこの死 = 粒子の崩壊であるなら、観察者 = ねこということになって、箱の覆いをとる前から (粒子が崩壊して青酸ガスが放出された時から) ねこは生きているか死んでいるか、観測されている (重ね合わせ状態ではなくなっている) のではないかと思っちゃうんですよ。
ねこが自分自身の観察者たり得ない理由って何なんでしょうか?
【言い訳っぽい解答】
ちょっと状況を変えてみましょう。猫を箱に入れる変わりに、白い玉を入れることにします。そして青酸ガスの変わりに赤いペンキを吹き付けることにします。つまり、粒子$A$が崩壊すると玉は赤くなると考えてください。(多少ムラができるだろうというのは思考実験だからなしにします。)
すると状況は以下のように変わります。
1時間後の玉の状態は、白$50\%$と赤$50\%$の重ね合わせになります。決してピンクの状態ではありません。さらに玉に意思はありませんから、純粋に、観測するまで玉の状態は誰も知りません。これなら納得できるでしょうか?
覆いをとって玉を観測した瞬間、玉の色は、白か赤かに決まります。それ以前は、重ね合わせとしか理解できない、と言うのが量子論の立場です。「猫」すなわち「意識を持っている」と考えるので、猫には解ってしまう、ということを考えてしまうわけで、「玉」なら問題ないだろう、というのがこの解答の趣旨です。
絶対、そういう答えを期待しているんじゃない、よねえ。
【さらなる疑問】
もし覆いを半分しかかけないで、覆いのある側に$X$という人がおり、覆いのない側に$Y$という人がいるとする。実験の$1$時間後の状態はどうなるか?
$X$氏にとっては、状況は今までと同じ。「猫」は生きている状態と死んでいる状態の重ね合わせです。ところが、$Y$氏には全てが見えています。従って$1$時間後の「猫」は、生きているのか死んでいるのか、$Y$氏には確定している、これはいったいどのように解釈すれば良いのでしょう。
さらに話を複雑にします。$Y$氏と$X$氏の間でサインが決めてあり、「猫」が死んだら、$Y$氏は$X$氏にサインを送ることにします。すると、$X$氏には「猫」の状態を見ていないのに「猫」の死が解ってしまう、という状態が発生します。これはどのように解釈すれば良いのでしょう。
【答えでない解答】
ここまで来ると、もう観測、という問題は、それをどのように考えるか、という解釈の問題だけになってしまいます。
「我観測す故に粒子あり」
次章、「EPR論文をめぐって」は、この章と大いに関係する。
次章へ 一言いいたい!

目次へ 次へ進む 前へ戻る

沖田十三
1.波動関数
量子論において有名な「猫」の話をするには、前置きが必要で、しかも長い。しかし、みなさんはしっかりその前置きに耐え、無事「猫」の問題にたどり着けることを信じて疑わない。
まず、第一の前置きであるが、「波動関数」である。(あっ、ここで読むのを止めようとした人がいるでしょう。ダメです!ちょっと付き合ってください。)
最初から余談
「宇宙戦艦ヤマト」は、『波動砲』なる必殺技を持っている。これを一発ぶっ放すと、全てが解決するという夢のような武器である。あたかも、ウルトラマンのスペシウム光線のようだ。(歳がばれますね、こんな話をしていると。)
『波動砲』とは、いったいいかなる「波動」を発射しているのだろうか? 影像によれば、ヤマトのエネルギー充填状態が$120\%$になると、艦長”沖田十三”が、「発射!」と叫ぶ。するとヤマトの艦前方に開いた穴から、炎のような束が前方に発射され、多くの場合、その束を浴びた物は、熔けるように爆破消滅してしまうのであった。
もし、波動が電磁波だったら、多分こんなことは起きない。高エネルギー電磁波(ガンマ線)の位相を合わせて、レーザーにしても、それを浴びた物体をレーザーが貫通したり、すぱっと切れることはあっても、熔け爆発することはないはずである。いったいあれは何の波動なのだろう? 疑問は尽きない。
閑話休題
波動関数とは、粒子の状態を数式で表したものである。
なんかおかしいと感じた人が必ずいると思う。
波動関数なのに、粒子? という疑問である。この「量子論」の話では、再三「物質は粒子であり、波である」と繰り返してきたのであった。だから、とりあえず、一番最初に言い訳をしておく。
粒子を波動関数で表現すると波動性が表れるということである。
そして、もうひとつ、
観測後に現れるであろう粒子の持つあらゆる状態を含んでいるということである。
波動関数は、他の物理関数のように、時間と位置を変数とする関数になっている。そしてこの関数はギリシャ文字のプサイ$(\psi)$で表す慣習になっている。
空間を何の束縛も受けず自由に直線運動をしている粒子の波動関数は、次のように表される。
$\Psi(t,x)=A\cos(\omega t-kx)+iA\sin(\omega t-kx)$説明しなくてもおわかりと思うが、$(t)$は時間、$(x)$は位置を表す。
説明しなくてもおわかりと思うが、$(\cos)$はコサイン、$(\sin)$はサインを表す。
説明しなくてもおわかりと思うが、$(i)$は虚数単位$\sqrt{-1}$を表す。
説明しないとわからないと思うが、$(A)$は波の振幅である。
説明しないとわからないと思うが、$(\omega)$は$(2\pi\nu)$である($\nu$は、ご承知の通り振動数である)。
説明しないとわからないと思うが、$(k)$は$(2\frac{\pi}{\lambda})$である($\lambda$は、ご承知の通り波長である)。
振動数$(\nu)$は、粒子のエネルギーに関係している。($E=h\nu$を思いだして!)
波長$(\lambda)$は、粒子の運動量に関係している。($p=\frac{E}{v}=\frac{h\nu}{v}=\frac{h(\frac{v}{\lambda})}{v}=\frac{h}{\lambda}$)
つまり波動関数は、物質の粒子としての側面と波動としての側面を全て持った関数である、ということが言える。
ここで、思考実験をする。今、上記で表される粒子と同じ速度で粒子と同じ方向に走っているとする。すると、コサイン、サインで表される正弦波は形を変えないはずである。そのはずである。
従って、
$(\omega t-kx)$は、一定値になるはずであるところが、
$(\omega t)$は時間と共に増えるはずであるよって、
$(kx)$も同じように増えなければならないことになる。
つまり時間と共に粒子は位置を変える、つまり静止してはいられない。これが、とりあえずの結論。
つまり、粒子であろうとも絶対に静止できない、これは、「不確定性原理」そのものである。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る
M.ボルン
2.幽霊波
前回、「空間を何の束縛も受けず自由に直線運動をしている粒子」の波動関数を説明した。それがきちんと理解できたか否かは大きな問題ではない。
状況によって、波動関数は様々な状態に変化しうる。前項のような単純(どこが単純じゃ!と思うかも知れないが)でない場合も多々ある。ただ最も単純な状況であっても、波動関数に、虚数項が入っていることに注目してもらいたい。
数式に虚数が現れる(複素関数である)と、物理では、それは「観測不能」であるということと同じ意味と捉える。その話を今回しようと思うわけであるが、この時点で意味を理解している人はいないはずである。具体例で話をする。
以前、ド・ブロイが「電子は波である」ことを提唱し、それが実験的に確認された、という話をした。
その実験とは、電子線を蛍光面へビーム状に発射するとき、電子源と蛍光面の間にスリットを置く、という簡単な実験である。
何のことだか理解不能という人は、まず図10−1をみてもらいたい。

ひとつ穴のスリットを通った電子線は、蛍光面に幅広くぼやけた像を結ぶ。この現象は、光でよく知られており、「回折」というものである。
次に、図10−2を見てもらいたい。

ふたつ穴のスリットを通った電子線は、蛍光面に筋状の縞模様を作る。この現象は、「干渉」と呼ばれる。
どちらも、波でなければ起こらない現象であり、ド・ブロイの電子波は、これらの実験で証明された。
ところで、この波動関数に物理的な解釈を求めたのがドイツの”ボルン”である。
後者の二重スリットの実験において、電子という一個の粒子は、スリットAか、スリットBのどちらかを通るはずであり、スリットの近くに検出装置を置いて観測すれば、どちらを通ったかを検出することができる(はずである)。従って、電子のとる状態は二種類あることになる。
(a)スリットAを通過するここまでは、誰も疑問をもたないはずである。これを波動関数で表すと、
(b)スリットBを通過する
$\psi(a)=$電子がスリットAだけを通過する状態となる。
$\psi(b)=$電子がスリットBだけを通過する状態
電子が二重スリットのどちらを通過したのかは、観測してみなければ解らないので、観測されない状態で、電子の状態を書き表せば、波動関数は、上記両者の重ね合わせとして、
$\Psi=\psi(a)+\psi(b)$のようになる。このように重ね合わせることができるのも、波の重要な性質である。
ただし、この重ね合わせの式は、たった一個の電子についてのものであることに注意してもらいたい。波動関数、$(\Psi)$や$(\psi)$は、複素関数なので、実在する波を表しているのではなく、数学的な波である。
ボルンは、この波動関数の2乗、すなわち
$|\Psi|^2$を、「電子の存在確率を表す」と解釈した。
$|\psi|^2$
どういうことかというと、波動関数$\psi(x)$を、電子が位置$(x)$にいる時の波動関数と考えれば、$|\psi|^2$は、電子が位置$(x)$に存在する確率であるということだ。
なぜ波動関数の2乗が出てくるかというと、2乗することにより虚数項が消えるからである。絶対値の記号$(|△|)$が出てくるのは、結果を必ず正の数にするための細工である。
細工と言っては、ボルンに失礼だ。測定に掛からない波動関数に対し、測定可能な2乗項を「確率」と見抜いたボルンの慧眼は特筆すべきである。(教育者としても、数々の物理学者を育てたボルン、アインシュタインとの親交も深く、「神はサイコロを振らない」という名言は、アインシュタインがボルンに当てた書簡で述べられた。米国の歌手であるオリヴィア・ニュートン・ジョンの祖父でもある。)
波動関数を2乗することで現れるこの確率はあくまで、電子一個に対する確率である。
$|\psi(a)|^2=$スリットAだけがあってBはふさがれているとき、電子が蛍光面にあたる確率ということがいえる。
$|\psi(b)|^2=$スリットBだけがあってAはふさがれているとき、電子が蛍光面にあたる確率
それでは、AとBの両方が開いているときは?
$|\psi(a)|^2+|\psi(b)|^2$であろうか?
実はこれではよくない。なぜ? これだと、回折模様が重なるだけで、干渉縞が出てこないからだ。
そこで、実際のAとBの両方が開いているときの波動関数は、
$|\psi(a)+\psi(b)|^2$となるのである。よって、二重スリットにおける電子通過の確率は
$|\Psi|^2=|\psi(a)|^2+|\psi(b)|^2+\psi(a)\psi^*(b)+\psi(b)\psi^*(a)$のようになる。頭の2項は、回折模様を表すが、後ろの二項は、プラスになったりマイナスになったりして、干渉縞を作ることになる。("$*$"には意味があるのだが、ここでは説明しない)
さて、蛍光面へ発射する電子の数が膨大になれば、この確率は一般の確率分布に従い、その結果、図に示したような回折模様や、干渉縞が現れることになることは納得できる。これは実験的にも確かめられている。ところが、上式は、一個の電子の波動関数であるという。ならば、この関数を素直に解釈すれば、一個の電子が、スリットAもBも通ることになってしまう。
これをどのように見るか?
観測される前の電子は、波動関数という複素関数なので、その状態は「解らない」のだ。ただ言えるのは、その波動関数の2乗が、一個の電子が、Aを通るかBを通るかの確率の重ね合わせになることである。
理解が難しくなって来た。要するに、観測される前の電子の状態は、波動関数という幽霊波なのである。どうやったって解らないのである。これを言い換えると、電子を観測したとたん、電子は実在として現れるから、波動関数という幽霊は消滅する。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

A.アインシュタイン
3.波動関数は光速を超えて
おさらいをする。
「物体」を「波」と捉えている間は、その「物体」は何ものか解らないのだ。それは波動関数という名の幽霊波(複素関数)だからである。「物体」を「粒子」と認識した瞬間、波動関数が消えて、そこに粒子が現れる。
これが、前回言ったことだ。
だから、波動関数としての電子波がどこを通ってそこに現れたのか、誰にも(たとえラプラスの悪魔であっても)解らんのだ。よいか、だからラプラスの悪魔は存在できないことになってしまうのだ。
「誰にも認識できないものは、物理学で相手にしてはいけない、と何度も言ったよなあ。この場合はどうしてくれる!」と怒らないでほしい。前回をちゃんと読んでくれた人には、次の事実がわかっているはずだ。
幽霊波である波動関数の絶対値の2乗は、「存在確率」という、現実の数値になる。ということを。
たくさんの電子が二重スリットを通り抜けるとき、それらの総和は、電子が蛍光面のどこへ到達するか、という確率になる。それが干渉縞なのだ。
ところが、これを1個の粒子に当てはめるから話はややこしくなってくる。(もともと波動関数は、個々の粒子状態を表すものであり、大量の粒子線の分布確率を表すものではない。)
そこで今回は、次のような思考実験をする。
ちょっと唐突かもしれないが、粒子$A$があって、これが粒子$B$と粒子$C$に崩壊すると考える。$B$と$C$の質量に違いがないとし、崩壊した粒子$(B、C)$は共に粒子$A$がいた場所から飛び去るとすれば、もし$B$、$C$を粒子として考えれば、運動量が保存されるのだから、$C$は$B$と逆方向に飛んで行くはずである。ここまではよいだろうか。
ところが、$B$、$C$を波として見ると、$B$も$C$も、$A$のいた位置からあらゆる方向へ伝播して行く波動関数である。どこを飛んでいるか解らないのだ。幽霊波たる所以である。
しかし、ある場所で、$B$を「粒子」として観測したとする。この瞬間、Bの波動関数は消滅する。$B$が実態として現れる。とりあえずここまではよい。
ところが、粒子としての$C$は、粒子$B$と逆方向へ走っていることが解っているのだから、粒子$B$を観測した瞬間、$C$の波動関数も消滅し、粒子$C$が姿を現すことになる。これは困った。
何が困った?
粒子$A$があった場所から、粒子$B$が観測された地点までの距離を仮に、$10$光年とする。なにが起きるか、粒子$B$が観測された瞬間、粒子$C$の場所が判明するのだから、「粒子$B$が観測されてしまった。」という事実は、瞬間的に粒子$C$を実体化させる。このとき、$B$と$C$が、$20$光年離れているという距離は関係なくなってしまう。
「粒子$B$が観測されて波動関数が消滅する」=「粒子$C$が実体化する」のであれば、粒子$B$の波動関数消滅は、光速を超えて、粒子$C$を実体化させる。
この宇宙で、光速より速いものはない、という相対論に反してしまう。
もちろん、”アインシュタイン”は、このことに大反対し、次のように主張した。
粒子$B$も$C$もはじめからある決まった方向へ進んでいるのだ。と。
それを知る手段をまだ我々は持っていないだけだ。
よって量子論はまだ不完全な理論だ。
もちろん不確定性原理も間違っている。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る


N.ボーア A.アインシュタイン
4.異議あり!
物体とは、「粒子として観測されるまでは、2乗すると存在確率となる波動関数、という波である」というのがボルンの下した結論であった。
その結果の解釈として「波動関数の消滅」(これを「波束の収縮」と呼ぶのが一般的なので今後はこの言葉を用いる)という現象が、時間を要しない、すなわち光速度を超えるという解釈を”アインシュタイン”が許すはずがない。そこで彼は、量子論の根底である「不確定性原理」を否定することで、「光速度を超えるもの」を間違いであると言おうとした。つまり「時間とエネルギー」の不確定を否定する思考実験が登場したのである。有名な「ボーアとアインシュタインの論争」である。
さて、アインシュタインは反論した、のであるが、なにしろ電磁波という明確な波が実は粒子としての側面を持っている、と言い出したのは、誰あろうアインシュタイン本人である。
光電効果を思いだしてもらいたい。波長の長い電磁波をいかにがんがん当てても飛び出さない電子が、ある波長より短くなると、ほんの少しの照射で飛び出す、という現象が光電効果である。
プランクは、これを次の式で表せることに気付いた。
$E=h\nu$つまり波(電磁波)は、その性質である振動数$(\nu)$に$h$(プランク定数)をかけた粒子と見なせるものである、と数式化したのであった。これは、アインシュタインも問題なく受け入れたのである。
だが、波束の収縮をアインシュタインは認めなかった。次の言葉が有名だ。
神は、サイコロ遊びをしないちょっと聞いただけでは何のことか解らないであろう。
波動関数は、間接的に粒子の存在確率を表すものである神様は確率的にしか示されないような(サイコロを振って居場所を決めるような)変な波は作らない、というのがアインシュタインの言いたいことだった。
観測されるまで、粒子は存在確率だけを持った幽霊波なのである
神様でさえ(ラプラスの悪魔でさえも)その粒子がどこにいたかを示すことはできない
アインシュタインは、実は全ては決定されている、というラプラスと同じ考えを持っていたのだ。つまり、粒子が観測された時、その粒子がたどってきた道のりは決まっているのだと考えた。それが現在の我々には示せないだけであると主張した。それは量子論がまだ不完全である証拠とまで言い切った。
今思えば、この点に関してはアインシュタインも実に保守的な物理学者であった。この意味で相対論ですら古典物理と言われるのである。
私は、アインシュタインが保守的な物理学者であったというよりは、あまりにも孤高の物理学者であろうとし過ぎたのではないかと考えている。特殊相対論と一般相対論を一人で創りあげ、晩年は、電磁波と重力を一本化する方法(大統一理論)に取り組んだほどの独立独歩の物理学者である。
ところが、量子論は一人では創れない、そういう理論であったことを証明したのが”ボーア”であった。コペンハーゲンに花開いた量子論は、彼が集めた若手物理学者達の群れから浮かび上がって来たものである。
粒子が量子として観測されるまでは、それが確率的にしか示せない存在である、というのが波動関数を不確定性原理に置き換えたものである。そして四元物理量の導入により、それが時間とエネルギーの不確定関係になる。言い換えれば、四次元時空間上の一点を占める粒子は、そのエネルギーも運動量も確率的に決定されるものであって、それ以上のなにものでもない、ということだ。
アインシュタインはこの「時間とエネルギー」の不確定を否定する思考実験をボーアに突きつけた。時に1927年のことである。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

思考実験の図
5.思考の対決
アインシュタインが持ち出したのは、シャッターのついた箱をつるしたバネ秤であった。箱の中には、光という形でエネルギーが存在すると考える。シャッターを開けるとそこから光が飛びだす。アインシュタインはこの思考実験で次のように主張した。
(1)シャッターを開ける前の箱のエネルギーは、時間さえかければ好きなだけ正確に測定できる。
(2)箱のシャッターを開けて光(エネルギー)を放出する
(3)光を放出後のエネルギーも(1)同様好きなだけ正確に測定できる
(4)よって、放出されたエネルギーはいくらでも正確に測定できる。
(5)これは、光を放出した時間(シャッターを開けた時間)に依存しない。
(その気になれば、シャッターを開ける時間をいくらでも小さくできるのだから)
(6)よって、$(\Delta E=0)$でも$(\Delta t=0)$が可能である。
いかがであろうか。思考実験の創始者たるアインシュタインである。よく考えられたものだと感じないだろうか?
これには、ボーアも困ったらしい。一晩徹夜して答えを考えたと言われている。
なんとボーアの反論はアインシュタインの一般相対論を逆手に取った次のようなものである。
(1)バネ秤で、質量を正確に測るということは、バネの延びを前提としている
(2)バネが延びて箱が下がると、これが地球上では、前後で重力加速度が変わる
(3)重力加速度が変われば、時計の進みが変わるのは、一般相対論の結論である。
(4)よってバネの延びを限りなくゼロに近づけることが、時間を正確に測ることの条件である
(5)バネの延びが限りなくゼロに近づけば、質量(エネルギー)は測れない
以上の論理で、$(\Delta t)$と$(\Delta E)$の不確定性を、一般相対論を用いて反論したのである。
大方の意見は、ボーアの判定勝ちである。なんとなく論点がずれたところでの空中戦のような気がしないでもない。しかし不確定性原理は依然として健在であり、従って波動関数もまた生きている。
では、波束の収縮はやはり光速を超えるのか?実はボーアもこれには答えていない。
それ以前に、波束の収縮というのは、物理的な現象なのか?
「波束の収縮についてきちんと説明できない理論は不完全だ。」もしかするとアインシュタインが言いたかったのもこの事だったのかもしれない。波動関数という数式をどのよういじくり回しても、波束の収縮に繋がる解は得られないのである。したがって、波束の収縮は未だに解明されていない謎、と言う人もいる。
しかし現実にはこの解釈は違う、と私は考えている。観測すると粒子が現れた。それならば、その前の事なんてどうでもいいではないか。これが波束の収縮に対する答えである。
観測される前の状態を記述するのが量子論の波動関数なのであるという立場をとるのである。言い換えると、粒子の観測によって波束が収縮するのではなく、不要になるのだ。それだけの話。
観測されてしまったものに、波動関数をあてはめようとすることが、そもそもナンセンス
さて、量子論の神髄が少しずつ見えてきた。シュレーディンガーの波動方程式の話をすれば、「猫」はすぐそこにいる。というよりも、ここまでの議論の中にも「猫」はチラチラ姿を現しているのだ。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

E.シュレーディンガー シャーロック・ホームズ
6.シュレーディンガーの波動方程式
おさらいをしておこう。(しつこい、と思うかもしれないが、何度言っても解ったようで解らない気分の人が多いはず)
時空間を走る、ある粒子について、アインシュタインはこう言った。
それは実在する粒子であって、隠れた秩序に従っている。ただ我々が完全な秩序を知らないだけだ。
ボーアは次のように言った。
それは、私の観測によって創造された実在体験なのだ。私が見るまでそれは存在しなかったのだ。
それでは、水素原子の周りの電子について考えてみよう。
古典物理では、長岡半太郎が予言したような惑星モデルで水素原子が説明される。すなわち、プラスの電気を持った原子核の周りをマイナスの電気を持った電子が回っているというモデルである。
ところが、ド・ブロイにより電子も波であることが提唱され、それが確認された。
電子も、それが観測されるまでは、波動関数で示される複素関数であった。これを数式化したのは、オーストリアの物理学者”シュレーディンガー”である。
写真を見てほしい。パイプに火を付けようとしているその姿は、シャーロック・ホームズの風貌そのものではないか。
大学で物理を始める前は、自然科学のみならず古典言語の文法や詩、そしてドイツの哲学者ショーペンハウエルを読みふけったそうである。後に「シュレーディンガーの猫」の思考実験を提示したのも、哲学書の影響であろうか。
そんな彼が示したのが、かの有名な「シュレーディンガーの波動方程式」である。
波として見たときの粒子は波動関数である。しかし波動関数そのものが単純な形で数式化されない場合は、時間および空間に関する微分方程式を解かないと、波動関数そのものが明確にならない。このときの波動関数を導く方程式を波動方程式という。シュレーディンガーは、電子波が満足すべき波動方程式があるとすれば、電子の粒子としての属性$(E=h\nu)$と波動としての属性$(p=\frac{h}{\lambda})$の双方を満足させる必要があると考えた。
その結果導かれたのが次の方程式である。
$i\hbar\frac{\partial\psi}{\partial t}=\frac{\hbar^2}{2m}(\frac{\partial^2\psi}{\partial x^2}+\frac{\partial^2\psi}{\partial y^2}+\frac{\partial^2\psi}{\partial z^2})+U(x,y,z)\psi$$(\hbar)$の記号は『エイチバー』と読み、プランク定数$(h)$を$(2\pi)$で割ったものである。
$U$は、ポテンシャルエネルギーを表し.... と煩わしい説明はしないから、安心してほしい。
但し、次のことだけは、確認しておいてほしいのである。
この方程式を解くと求められるのは$(\psi)$である。これは電子波(波動関数)である。つまり、シュレーディンガーの波動方程式を解くと、水素原子の周りの電子の波動関数を求めることができる。
電子の波動関数を2乗すると、存在確率が求められるのであるが、これを素直に受け止めると奇妙なことになる。
今まで電子が回っているだろう、と思われていた軌道で最も存在確率が高く、そこから外れるにつれ徐々に存在確率が小さくなって行く、まるで雲のように見える妙な図が描かれる。

(実際の電子軌道は球面だから、本当はもっと絵にも描けないものである。)
しかも、この図が完全な電子の様子を示している訳ではない。あくまで、波動関数を$2$乗した確率分布が図のようになるだけなのである。
はいこの次は「猫」。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

シュレーディンガーの猫
7.「猫」の生死
シュレーディンガーの波動方程式から導かれる波動関数が、ある場合には水素原子の周りを回る電子の振る舞いを表すことは、前回までに述べた。その波動関数を2乗すると、前項で示した図のような電子雲で表現される存在確率の分布図として得られることも理解できたと思う。
電子の分布図は、次の二種類の解釈ができる。
(1)水素原子の周りで何度も電子を観測すると、その分布が図のようになる。普通に考えれば(1)が理解し易いと思うが、量子論の結論は(2)である。つまり分布図は、まだ点々が見えているが、実際には点ではなく限りなく霧に近いものであって、点の集合ではない、ということだ。
(2)水素原子の周りの1個の電子は、波動関数の2乗に従う確率で発見される。
さらに、霧のように観測される電子雲は、あくまで波動関数という複素関数の2乗である。実際には、霧のようなモノですらない。これを最終的にどのように捉えるかという問題は、シュレーディンガーの波動方程式が発表された時から存在した。
シュレーディンガー方程式から導かれる波動関数は、ある粒子のすべての状態の重ねあわせとして表現される。したがって水素原子の周りの電子は、原子核から無限に離れたところに存在するという状態、電子から一定の軌道上に存在する状態、原子核のごく近いところに存在する状態、・・・、というすべての場所に存在する場合の重ね合わせになる。
このとき、その状態の2乗をとってみると、「一定の軌道上に存在する状態」が一番大きくなるということが言えるのである。
この状況をもう少し単純化して提示してみよう。
ある粒子$A$が存在する。この粒子が$1$時間以内に崩壊する確率が$50\%$である、とする。これをどう見るか?
(a)多数の粒子$A$を用意すると、1時間後には半分の粒子が崩壊している。この二つの見方がある。まあ、ここまでは、上記(1)(2)に対応している。単に見方の違いである。
(b)1の粒子$A$は、1時間以内に$50\%$の確率で崩壊する。
であるが、この粒子$A$を用いて次のような思考実験を行うとどうなるか。
粒子$A%$をある容器のなかに入れる。これが、「シュレーディンガーの猫」と言われる問題である。
容器の中には、粒子$A$が崩壊したことを知るための検知器を入れる。
検知器が粒子$A$の崩壊を検知すると、青酸ガスが容器中に放出される。
容器内部が見えないように周りを覆う。
容器内に猫を入れる。
1時間後、容器の中の猫は生きているか、死んでいるか?
動物愛護の観点から上記のような実験は許されない!と叫ばないでほしい。だから思考実験なのだ。
(a)の立場をとれば、猫が生きている確率は$50\%$である。
ところが、
(b)の立場をとれば、猫が生きている状態が$50\%$、死んでいる状態が$50\%$
というへんてこりんな状況が出現する。
(a)の立場をとる人は、こう主張する。
「猫は、生きているか、死んでいるかのどちらかである。その確立は五分五分だ」
(b)の立場をとる人の主張はこうである。
「猫は生きているという状態と死んでいるという状態を同じ程度に重ね合わせた状態だ」
勘違いしてはいけない、(b)の立場は、猫が半死半生であると言っているのではない。「明確に生きている猫」と「全く死んでいる猫」が重ね合わされた状態であるというのだ。
生きている状態と死んだ状態をどちらも持っている? そんな猫がいるのか?
それだけではない。覆いをとって「猫」の状態を見たとたんに、猫の状態は「生」か「死」に決定するということである。
なんだか話が解らなくなってきた?
でも量子論の神髄を当てはめると、上記のような状態が出現する。
覆いをとって、「猫」の状態を見るまでは、「猫は生きているし、死んでいる」という状態である。「生きているか、死んでいるかどちらかだが、その確率は五分五分だ」という状態とは明確に区別される。
アインシュタインは、上記(a)の立場をとり、「神様は、サイコロ遊びをしない」と言った。しかしボーアに代表されるコペンハーゲンで学んだ物理学者たちは、(b)の立場をとって「観測されるまでは、すべての状態の重ね合わせである」という立場になるのである。
つまり「猫の生と死」も波動関数という複素関数で表される波になってしまう。 どちらが正しいか?
明確な答えは、現在でも出ていない。
一言いいたい!

【なにはさておき量子論 第6章 シュレーディンガーの猫】
目次へ 次へ進む 前へ戻る

デカルト
8.名問・珍解
実は、前項でこの章を終わるつもりだったが、なにか今ひとつ言い足りない気がしていた。そこへ絶好の質問をいただいたので、これに答えることで、「シュレーディンガーの猫」に対する補足説明としたい。
【質問】
なんで、シュレーディンガーが、件(くだん)の箱の中に生き物、それもねこなんて入れたのかは知りませんが、いつも違和感を覚えてしまうのはその部分です。
生きている状態と死んでいる状態の重ね合わせ、となったねこを想像できないんですよね。
言葉を介しての意思の疎通は出来ませんが、ねこにも意識があるだろうということはわかるわけで、だったら、自分が死んでしまったらそのことも多分わかるのではないかと思うわけで、ねこの死 = 粒子の崩壊であるなら、観察者 = ねこということになって、箱の覆いをとる前から (粒子が崩壊して青酸ガスが放出された時から) ねこは生きているか死んでいるか、観測されている (重ね合わせ状態ではなくなっている) のではないかと思っちゃうんですよ。
ねこが自分自身の観察者たり得ない理由って何なんでしょうか?
【言い訳っぽい解答】
ちょっと状況を変えてみましょう。猫を箱に入れる変わりに、白い玉を入れることにします。そして青酸ガスの変わりに赤いペンキを吹き付けることにします。つまり、粒子$A$が崩壊すると玉は赤くなると考えてください。(多少ムラができるだろうというのは思考実験だからなしにします。)
すると状況は以下のように変わります。
1時間後の玉の状態は、白$50\%$と赤$50\%$の重ね合わせになります。決してピンクの状態ではありません。さらに玉に意思はありませんから、純粋に、観測するまで玉の状態は誰も知りません。これなら納得できるでしょうか?
覆いをとって玉を観測した瞬間、玉の色は、白か赤かに決まります。それ以前は、重ね合わせとしか理解できない、と言うのが量子論の立場です。「猫」すなわち「意識を持っている」と考えるので、猫には解ってしまう、ということを考えてしまうわけで、「玉」なら問題ないだろう、というのがこの解答の趣旨です。
絶対、そういう答えを期待しているんじゃない、よねえ。
【さらなる疑問】
もし覆いを半分しかかけないで、覆いのある側に$X$という人がおり、覆いのない側に$Y$という人がいるとする。実験の$1$時間後の状態はどうなるか?
$X$氏にとっては、状況は今までと同じ。「猫」は生きている状態と死んでいる状態の重ね合わせです。ところが、$Y$氏には全てが見えています。従って$1$時間後の「猫」は、生きているのか死んでいるのか、$Y$氏には確定している、これはいったいどのように解釈すれば良いのでしょう。
さらに話を複雑にします。$Y$氏と$X$氏の間でサインが決めてあり、「猫」が死んだら、$Y$氏は$X$氏にサインを送ることにします。すると、$X$氏には「猫」の状態を見ていないのに「猫」の死が解ってしまう、という状態が発生します。これはどのように解釈すれば良いのでしょう。
【答えでない解答】
ここまで来ると、もう観測、という問題は、それをどのように考えるか、という解釈の問題だけになってしまいます。
他人がすでに観測してしまったら、もう自分の観測は無意味であるのか。「我思う故に我あり」、”デカルト”の言うとおり観測者の意思が、この宇宙の全ての事象を意味づける、と言ってもいいかもしれません。
本当に自分がこの目でみることが観測であるのか。
観測を間接的に他人から教えてもらってもそれは観測であるのか。
「我観測す故に粒子あり」
次章、「EPR論文をめぐって」は、この章と大いに関係する。
次章へ 一言いいたい!
